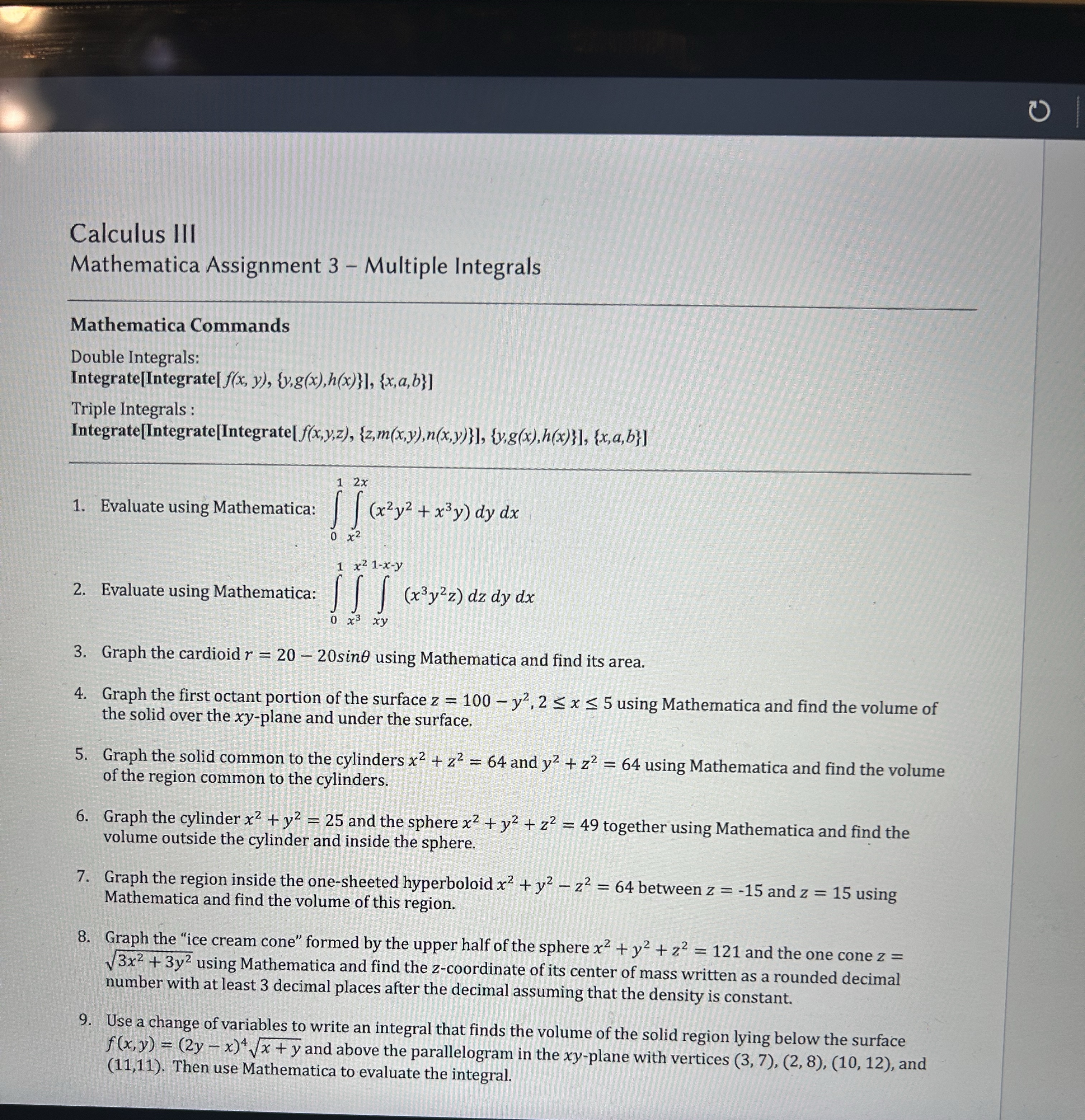
Calculus III

Mathematica Assignment $3-$ Multiple Integrals

Mathematica Commands

Double Integrals:

Integrate$[$Integrate$[f(x,y),\{y,g(x),h(x)\}$

Triple Integrals :

Integrate$[$Integrate$[$Integrate$[f(x,y,z),\{z,m(x,y),n(x,y)\}$

Evaluate using Mathematica: ${\displaystyle \underset{0}{\overset{1}{}}}{\displaystyle \underset{x^2}{\overset{2x}{}}}(x^2{y}^2+x^{3}y)dydx$

Evaluate using Mathematica: ${\displaystyle \underset{0}{\overset{1}{}}}{\displaystyle \underset{x^3}{\overset{x^2}{}}}{\displaystyle \underset{xy}{\overset{1-x-y}{}}}(x^3{y}^{2}z)dzdydx$

Graph the cardioid $r=20-20sin$ using Mathematica and find its area.

Graph the first octant portion of the surface $z=100-y^2,2x5$ using Mathematica and find the volume of the solid over the $xy-$plane and under the surface.

Graph the solid common to the cylinders $x^2+z^2=64$ and $y^2+z^2=64$ using Mathematica and find the volume of the region common to the cylinders.

Graph the cylinder $x^2+y^2=25$ and the sphere $x^2+y^2+z^2=49$ together using Mathematica and find the volume outside the cylinder and inside the sphere.

Graph the region inside the one$-$sheeted hyperboloid $x^2+y^2-z^2=64$ between $z=-15$ and $z=15$ using Mathematica and find the volume of this region.

Graph the "ice cream cone" formed by the upper half of the sphere $x^2+y^2+z^2=121$ and the one cone $z=\sqrt[\phantom{2}]{3x^2+3y^2}$ using Mathematica and find the $z-$coordinate of its center of mass written as a rounded decimal number with at least $3$ decimal places after the decimal assuming that the density is constant.

Use a change of variables to write an integral that finds the volume of the solid region lying below the surface $f(x,y)=(2y-x{)}^4\sqrt[\phantom{2}]{x+y}$ and above the parallelogram in the $xy-$plane with vertices $(3,7),(2,8),(10,12),$ and $(11,11).$ Then use Mathematica to evaluate the integral.