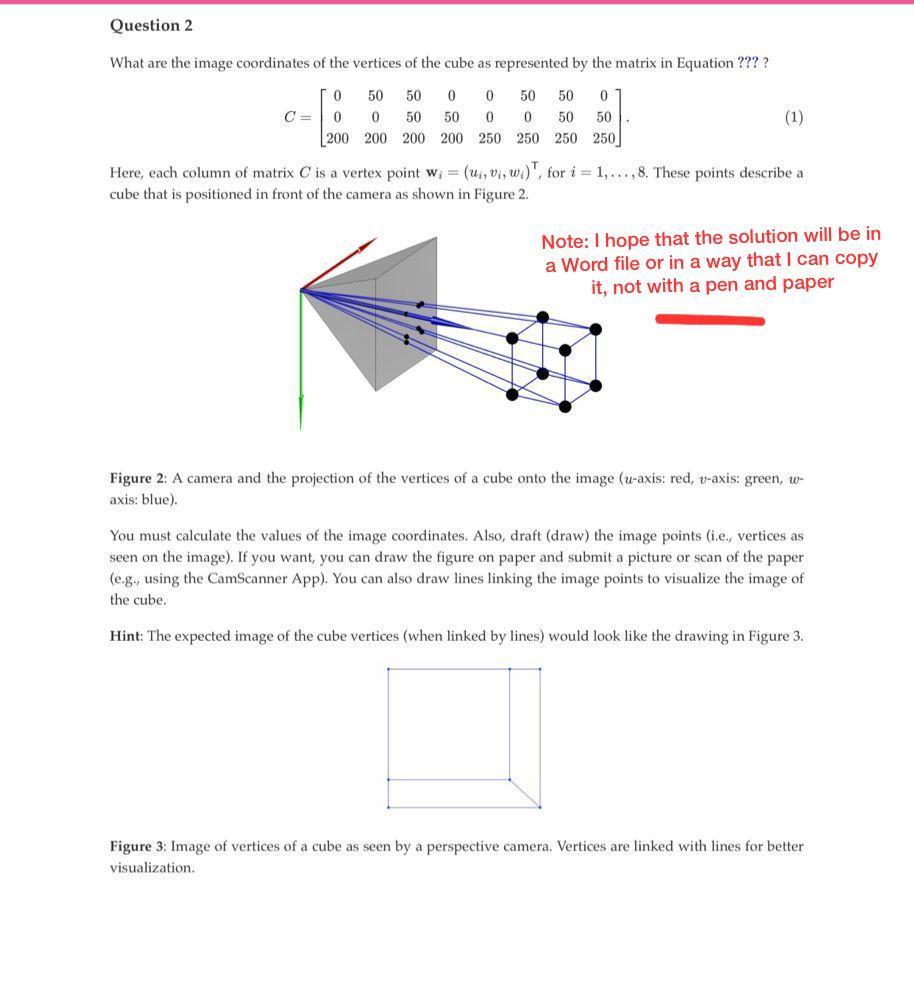
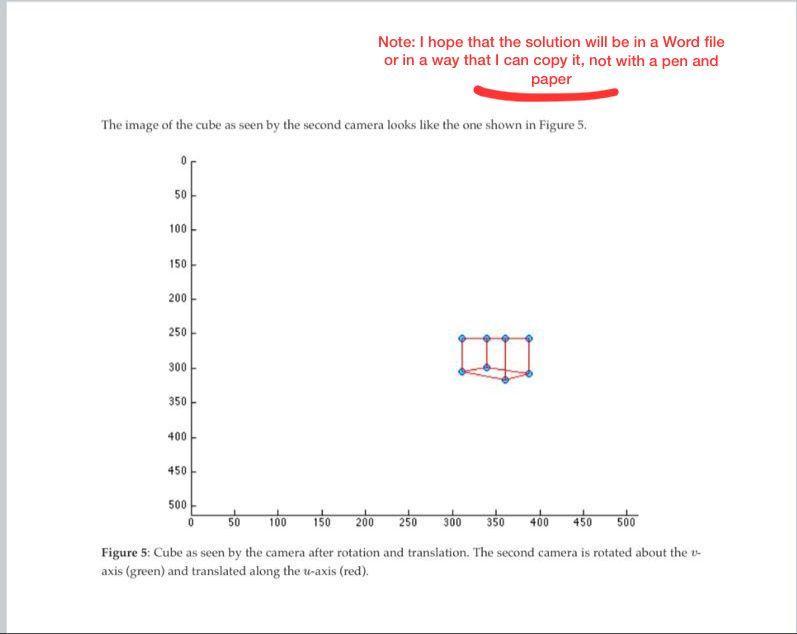
Camera model assignment Consider a perspective camera (i.e., pinhole camera) that acquires images of size 512 x 512 pixels, and is described by the following intrinsic parameters: Note: I hope that the solution will be in a Word file or in a way that I can copy it, not with a pen and paper skew factor: 0 . principal point: (256,256) focal distances: (200,200) Figure 1 illustrates a perspective camera as it projects a 3-D point onto the image plane. Figure 1: A perspective camera and the projection of a 3-D point onto the image (u-axis: red, v-axis: green, w- axis: blue). The center of projection is at the origin of the camera coordinate frame, which in this case coincides with the global coordinate frame (i.e., world coordinate frame). Question 1 What are the image coordinates x = (x, y) of the 3-D point w = (-50, 20, 200) projected under the camera? Hint: The perspective projection of a point w = (u, v, w) to an image point x = (x, y) is modeled by Equation 14.5 (Prince). This equation only accounts for the intrinsic parameters (i.e., transformations that happen inside the camera only). Question 2 What are the image coordinates of the vertices of the cube as represented by the matrix in Equation ???? 0 50 50 0 50 50 0 0 0 50 50 0 0 50 50 200 200 200 200 250 250 250 250 0 C = (1) Here, each column of matrix C is a vertex point w = (ui, vi, w), for i=1,...,8. These points describe a cube that is positioned in front of the camera as shown in Figure 2. Note: I hope that the solution will be in a Word file or in a way that I can copy it, not with a pen and paper Figure 2: A camera and the projection of the vertices of a cube onto the image (u-axis: red, v-axis: green, w- axis: blue). You must calculate the values of the image coordinates. Also, draft (draw) the image points (i.e., vertices as seen on the image). If you want, you can draw the figure on paper and submit a picture or scan of the paper (e.g., using the CamScanner App). You can also draw lines linking the image points to visualize the image of the cube. Hint: The expected image of the cube vertices (when linked by lines) would look like the drawing in Figure 3. Figure 3: Image of vertices of a cube as seen by a perspective camera. Vertices are linked with lines for better visualization. Question 3 Considering the same camera given in the previous questions and the cube vertices from Question 2, calculate the image coordinates of the vertices given that the camera now rotated by 35 degrees about the t-axis and translated along the u-axis by the following vector = (200,0,0). Figure 4 shows the original camera and the rotated camera. Figure 4: Original and rotated cameras pointed at a cube in space. The second camera is rotated about the u- axis (green) and translated along the u-axis (red). In this case, Equation 14.5 (Prince) would not work directly on the vertices coordinates given in matrix C. Before we can apply Equation 14.5, we need to remove the effects of the camera rotation and translation that took place. This can be done by considering the full perspective projection model, which accounts for the camera motion (i.e., extrinsic parameters). Note: I hope that the solution will be in a Word file or in a way that I can copy it, not with a pen and paper The full perspective camera is given by Equation 14.8. To use this Equation, you need the values of the rotation parameters wij in Equation 14.6. In Equation 14.7, the rotation parameters are represented by the general matrix 2, i.e.: [WI1 WI2 W13] = W21 W22 W23 W31 W32 W33. cos 0 0 9, 01 sin 00 In the case of this question, we need to use the rotation about the v-axis (equivalent to a y-rotation in the zyz- frame). The rotation about the v-axis is given by: -sin 6 0 cos 0 (2) (3) Keep in mind that the angle in these calculations should be given in radians and not in degrees. You must convert the angle from degrees to radians. The rotation angle 8 and the translation vector 7 are given. The image of the cube as seen by the second camera looks like the one shown in Figure 5. 50 100 150 200 250 300 350 400 450 500 Note: I hope that the solution will be in a Word file or in a way that I can copy it, not with a pen and paper 50 150 200 250 300 350 400 450 500 Figure 5: Cube as seen by the camera after rotation and translation. The second camera is rotated about the v- axis (green) and translated along the u-axis (red). 100