Can anyone help me to solve this 3. An application of the sampling distribution of the sample meanPeople suffering from hypertension, heart disease, or kidney problems may need to limit their intakes of sodium. The public health departments in some U.S. states and Canadian provinces require community water systems to notify their customers if the sodium concentration in the drinking water exceeds a designated limit. In Massachusetts, for example, the notification level is 20 mg/L (milligrams per liter).Suppose that over the course of a particular year the concentration of sodium in the drinking water of a water system in Massachusetts is not extremely nonnormal, with a mean of 18.3 mg/L and a standard deviation of 6 mg/L.Imagine that the water department selects a simple random sample of 30 water specimens over the course of this year. Each specimen is sent to a lab for testing, and at the end of the year the water department computes the mean concentration across the 30 specimens. If the mean exceeds 20 mg/L, the water department notifies the public and recommends that people who are on sodium-restricted diets inform their physicians of the sodium content in their drinking water.Use the Distributions tool to answer the following questions, adjusting the parameters as necessary.Normal DistributionMean =19.5Standard Deviation =0.85 1012141618202224xEven though the actual concentration of sodium in the drinking water is within the limit, there is a probability that the water department will erroneously advise its customers of an above-limit concentration of sodium.Suppose that the water department is willing to accept (at most) a 1% risk of erroneously notifying its customers that the sodium concentration is above the limit. A primary cause of sodium in the water supply is the salt that is applied to roadways during the winter to melt snow and ice. If the water department can't control the use of road salt and can't change the mean or the standard deviation of the sodium concentration in the drinking water, is there anything the depar

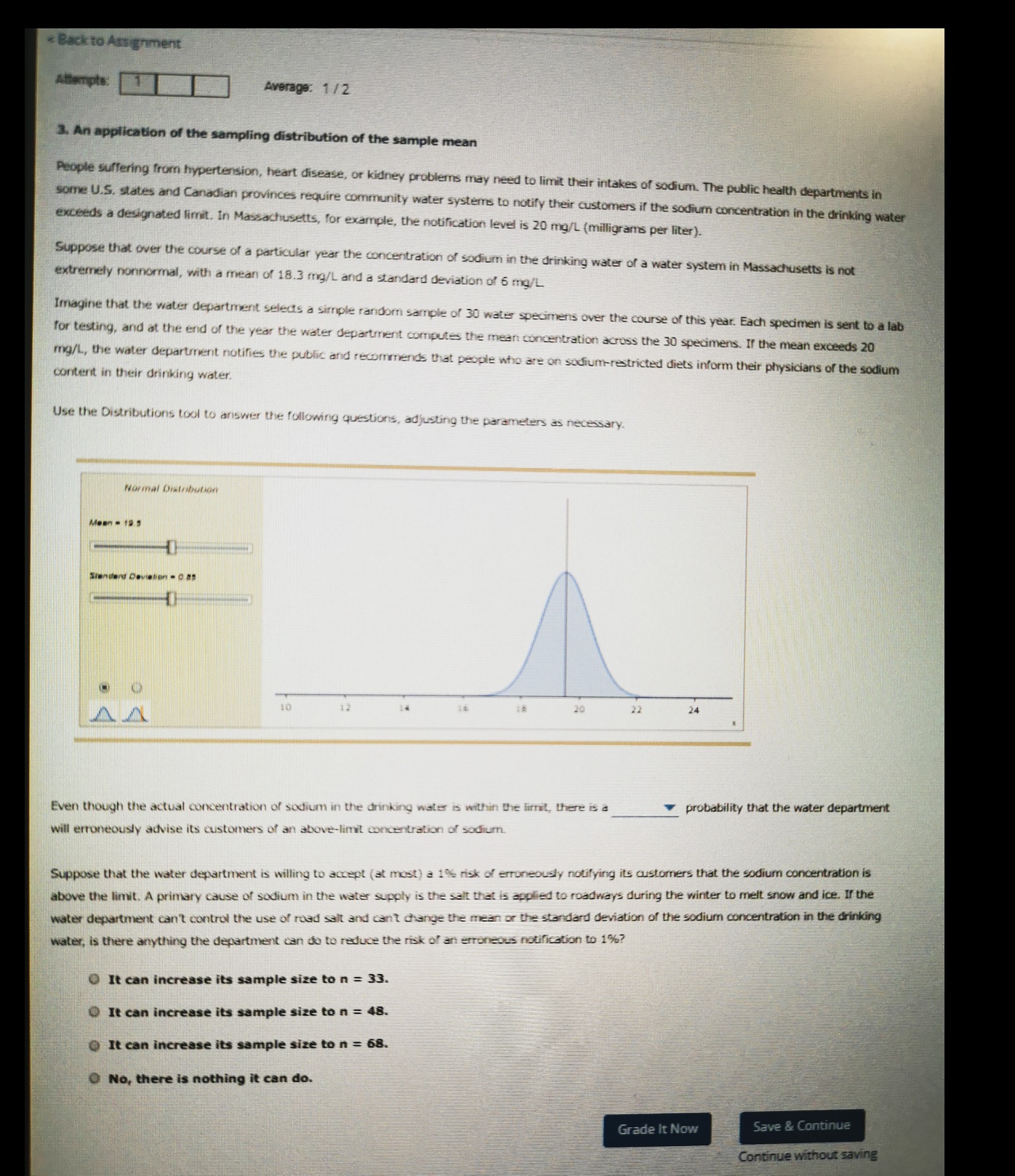
Back to Assignment Attempts Average: 1 / 2 3. An application of the sampling distribution of the sample mean People suffering from hypertension, heart disease, or kidney problems may need to limit their intakes of sodium. The public health departments in some U.S. states and Canadian provinces require community water systems to notify their customers if the sodium concentration in the drinking water exceeds a designated limit. In Massachusetts, for example, the notification level is 20 my/L (milligrams per liter). Suppose that over the course of a particular year the concentration of sodium in the drinking water of a water system in Massachusetts is not extremely nonnormal, with a mean of 18.3 mg/L and a standard deviation of 6 mg/L Imagine that the water department selects a simple random sample of 30 wates specimens over the course of this year. Each specimen is sent to a lab for testing, and at the end of the year the water department computes the mean concentration across the 30 specimens. If the mean exceeds 20 my/L, the water department notifies the public and recommends that people who are on sodium-restricted diets inform their physicians of the sodium content in their drinking water. Use the Distributions tool to answer the following questions, adjusting the parameters as necessary. Normal Diatobution 10 20 22 24 Even though the actual concentration of sodium in the drinking water is within the limit, there is a probability that the water department will erroneously advise its customers of an above-limit concentration of sodium. Suppose that the water department is willing to accept ( at most) a 1% risk of erroneously notifying its customers that the sodium concentration is above the limit. A primary cause of sodium in the water supply is the salt that is applied to roadways during the winter to melt snow and ice. If the water department can't control the use of road salt and can't change the mean or the standard deviation of the sodium concentration in the drinking water, is there anything the department can do to reduce the risk of an erroneous notification to 1%? It can increase its sample size to n = 33. It can increase its sample size to n = 48. It can increase its sample size to n = 68. O No, there is nothing it can do. Grade It Now Save & Continue Continue without saving