Can anyone please solve the question 14? It is a measure theory problem.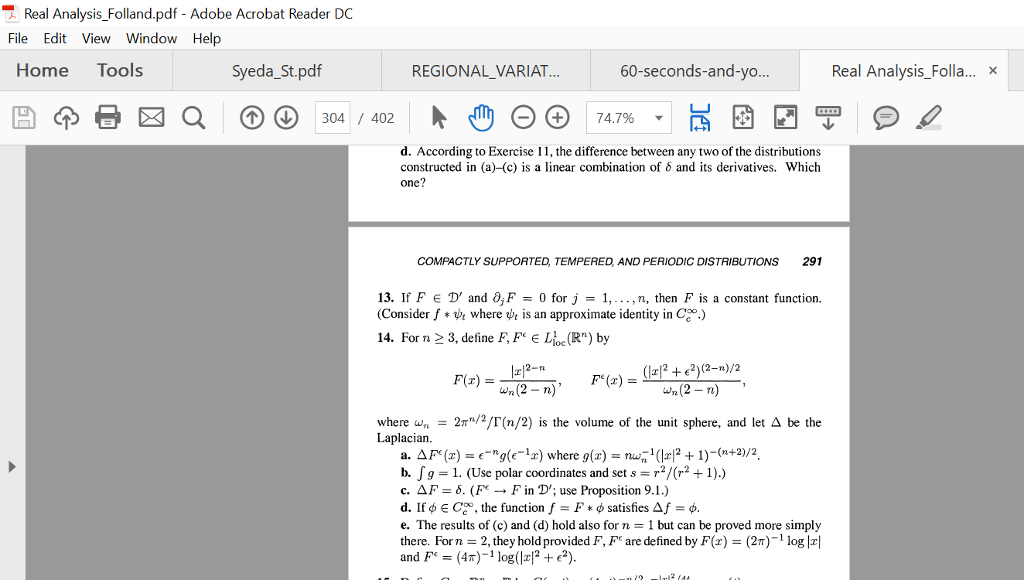

Real Analysis_Folland.pdf - Adobe Acrobat Reader DC File Edit View Window Help Home Tools Syeda_St.pdf REGIONAL_VARIAT... 60-seconds-and-yo... Real Analysis_Folla. X ?) (?) 304 / 402 - + 74.7% d. According to Exercise 11, the difference between any two of the distributions constructed in (a)-(c) is a linear combination of ? and its derivatives, which COMPACTLY SUPPORTED, TEMPERED AND PERIODIC DISTRIBUTIONS 291 13. If F E D' and 0,F 0 for j = 1, ,n, then F is a constant function. (Consider fe where is an approximate identity in Cc.) 14. Forn 3, define F, FE Lc(R) by wn(2 -n) where wn-2r"/2/rn/2) is the volume of the unit sphere, and let ? be the Laplacian a. ? Fe (z) = -ng(e-4) where 9(z) = n?1 (l 2 + 1)-(n+2)/2. b. fg-1. (Use polar coordinates and set/(r2 +1).) c. ?F-6. (P"- + F in D: use Proposition 9.1.) d. If ? Coo, the function f F * ? satisfies ?f e. The results of (c) and (d) hold also for 1 but can be proved more simply there. Forn 2, they hold provided F, F are defined byF (2T)1 log I and F (4)log( +e2). Real Analysis_Folland.pdf - Adobe Acrobat Reader DC File Edit View Window Help Home Tools Syeda_St.pdf REGIONAL_VARIAT... 60-seconds-and-yo... Real Analysis_Folla. X ?) (?) 304 / 402 - + 74.7% d. According to Exercise 11, the difference between any two of the distributions constructed in (a)-(c) is a linear combination of ? and its derivatives, which COMPACTLY SUPPORTED, TEMPERED AND PERIODIC DISTRIBUTIONS 291 13. If F E D' and 0,F 0 for j = 1, ,n, then F is a constant function. (Consider fe where is an approximate identity in Cc.) 14. Forn 3, define F, FE Lc(R) by wn(2 -n) where wn-2r"/2/rn/2) is the volume of the unit sphere, and let ? be the Laplacian a. ? Fe (z) = -ng(e-4) where 9(z) = n?1 (l 2 + 1)-(n+2)/2. b. fg-1. (Use polar coordinates and set/(r2 +1).) c. ?F-6. (P"- + F in D: use Proposition 9.1.) d. If ? Coo, the function f F * ? satisfies ?f e. The results of (c) and (d) hold also for 1 but can be proved more simply there. Forn 2, they hold provided F, F are defined byF (2T)1 log I and F (4)log( +e2)