Can someone answer this question with the script that provides under the above? Thank you.

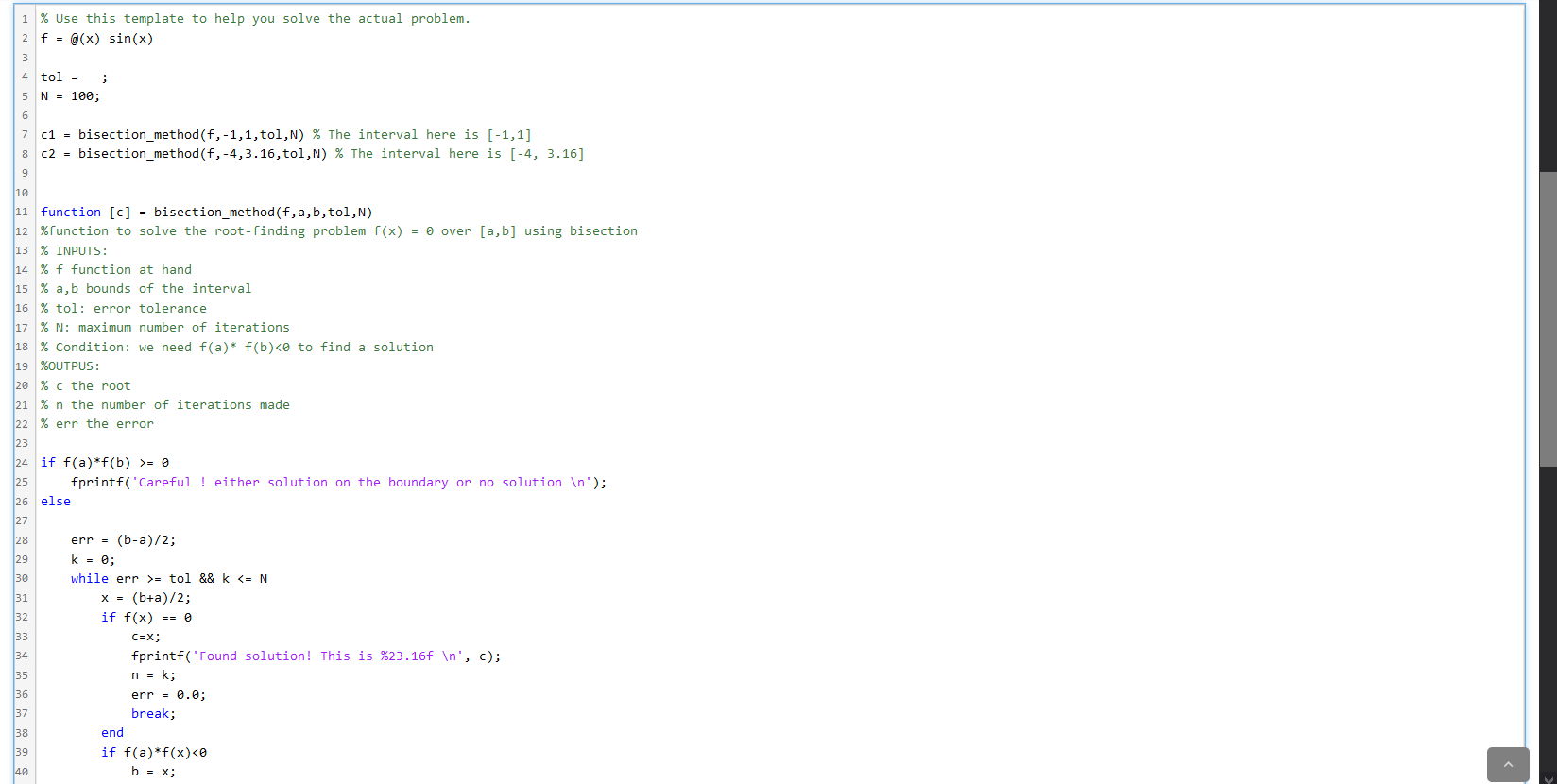
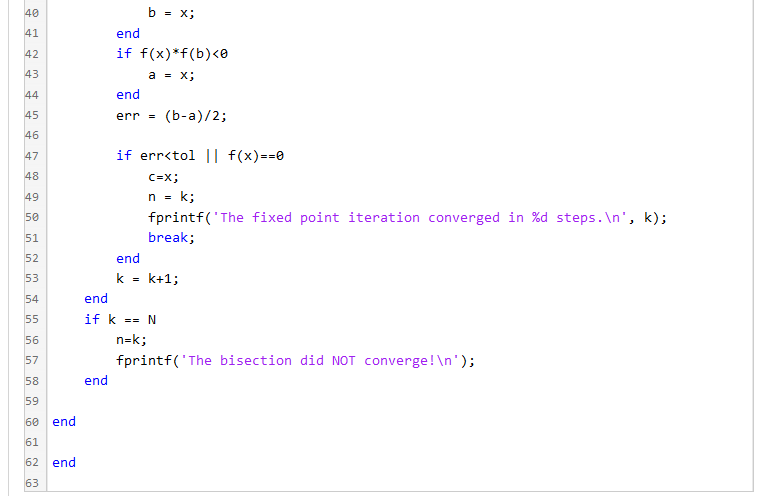
Bisection method on a complicated function O solutions submitted (max: Unlimited) Refer to the Learner Template of this problem to for an accuracy of 10^{-5} solve f(x) = (x+2). *(X+1).^2.**.*(x-1).^3. *(x-2) = for various intervals: (a) [a1, b1] = [-1.5,2.5] (b) [a2, b2] = [-0.5,2.4] (c) [a3, b3] = [-0.5, 3] (d) [a4, b4] = [-3,-0.5] What is the root for each case? Keep the maximum number of iterations the same for all cases. c1 = bisection_method(f, a1.b1, tol,N) c2 = bisection_method(f, a2,b2, tol,N) c3 = bisection_method(f, a3,63, tol,N) C4 = bisection_method(f, a4, b4, tol,N) No response needed: What does the bisection method applied to this problem tell you? Is the method sensistive to the interval you choose when the function has multiple roots/zeros? 1 % Use this template to help you solve the actual problem. 2 f = @(x) sin(x) 4 tol = ; 5 N = 100; RED 0 VOUW 7 c1 = bisection_method(f,-1,1, tol,N) % The interval here is [-1,1] C2 = bisection_method(f,-4,3.16, tol,N) % The interval here is [-4, 3.16] over [a,b] using bisection 11 function [C] = bisection_method(f, a,b, tol,N) 12 %function to solve the root-finding problem f(x) = 13 % INPUTS: 14 % f function at hand 15 % a,b bounds of the interval 16 % tol: error tolerance 17 % N: maximum number of iterations 18 % Condition: we need f(a) f(b)= 0 fprintf('Careful ! either solution on the boundary or no solution '); else err = (b-a)/2; k = 0; while err >= tol && k = 0 fprintf('Careful ! either solution on the boundary or no solution '); else err = (b-a)/2; k = 0; while err >= tol && k