Can someone help me solve this question? Please consider the hint : use the eigenvalues of A^TA. K2(A) is the condition number of A : the product of ||A||₂ * ||A^-1||₂

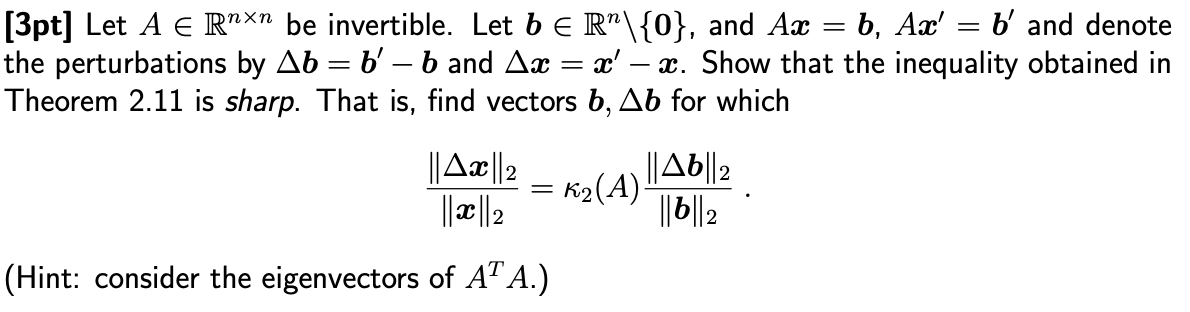
[3pt] Let A E Rx be invertible. Let b E R"\\ {0 }, and Ax = b, Ax' = b and denote the perturbations by Ab = b' - b and Aac = ac' - . Show that the inequality obtained in Theorem 2.11 is sharp. That is, find vectors b, Ab for which 1| A ac | 2 K2 ( A) 14b| | 2 1161/2 (Hint: consider the eigenvectors of AT A.)