Can someone help me to fix this

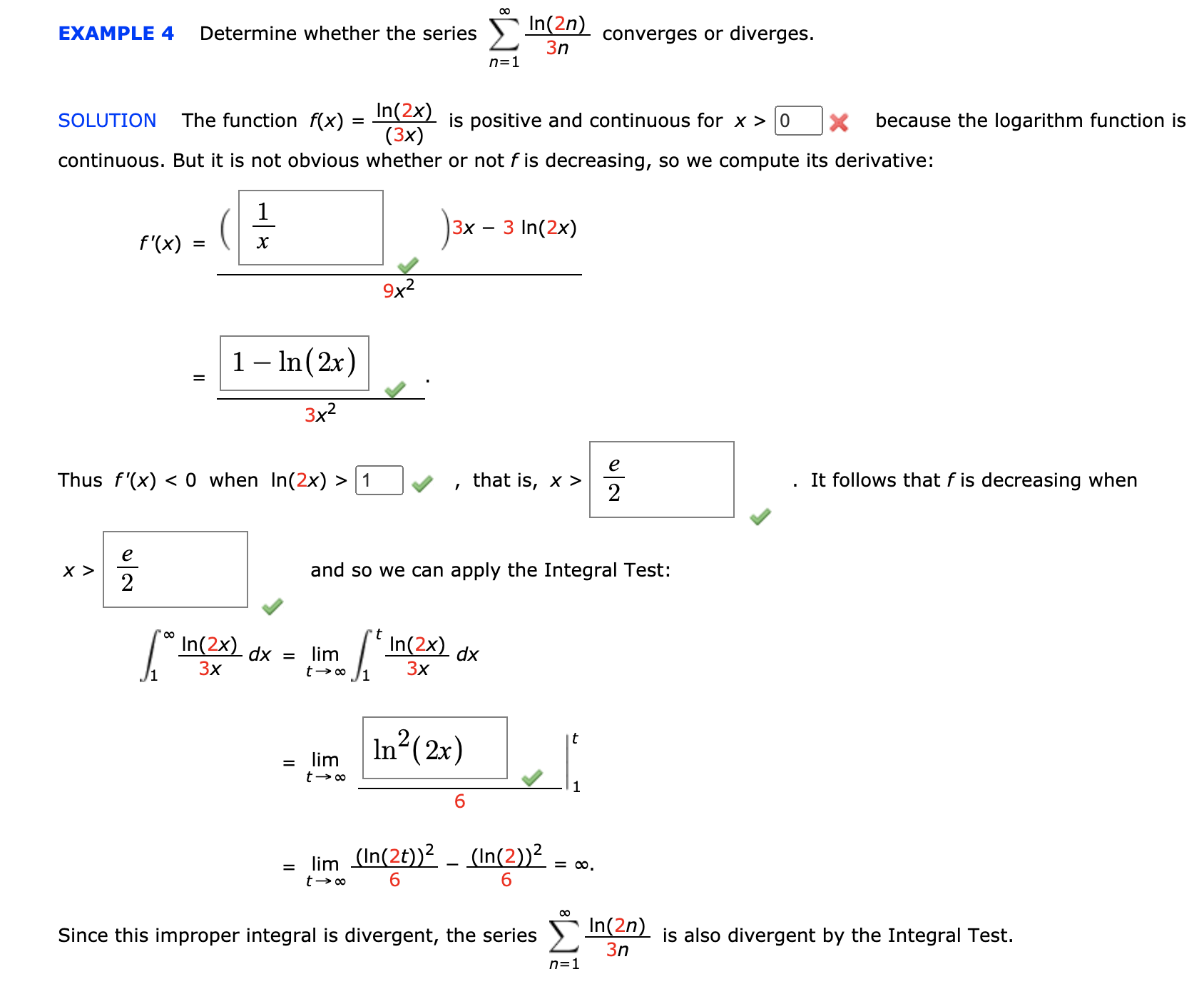
EXAMPLE 4 Determine whether the series In(2n) converges or diverges. n=1 3n SOLUTION The function f(x) = _ is positive and continuous for x > 0 X because the logarithm function is (3x) continuous. But it is not obvious whether or not f is decreasing, so we compute its derivative: f'(x ) = 3 x - 3 In ( 2 x ) 9 x2 1 - In(2x) 3 x2 Thus f'(x) 1 , that is, x> It follows that f is decreasing when NO and so we can apply the Integral Test: In(2X) dx = lim In(2x) dx 3x t -> 00 1 3X lim In" ( 2x) t - co 6 lim (In(2t))2 _ (In(2))2 t -> 6 6 - = 00. Since this improper integral is divergent, the series In(20) is also divergent by the Integral Test. n=1 3n