I need help with the following:

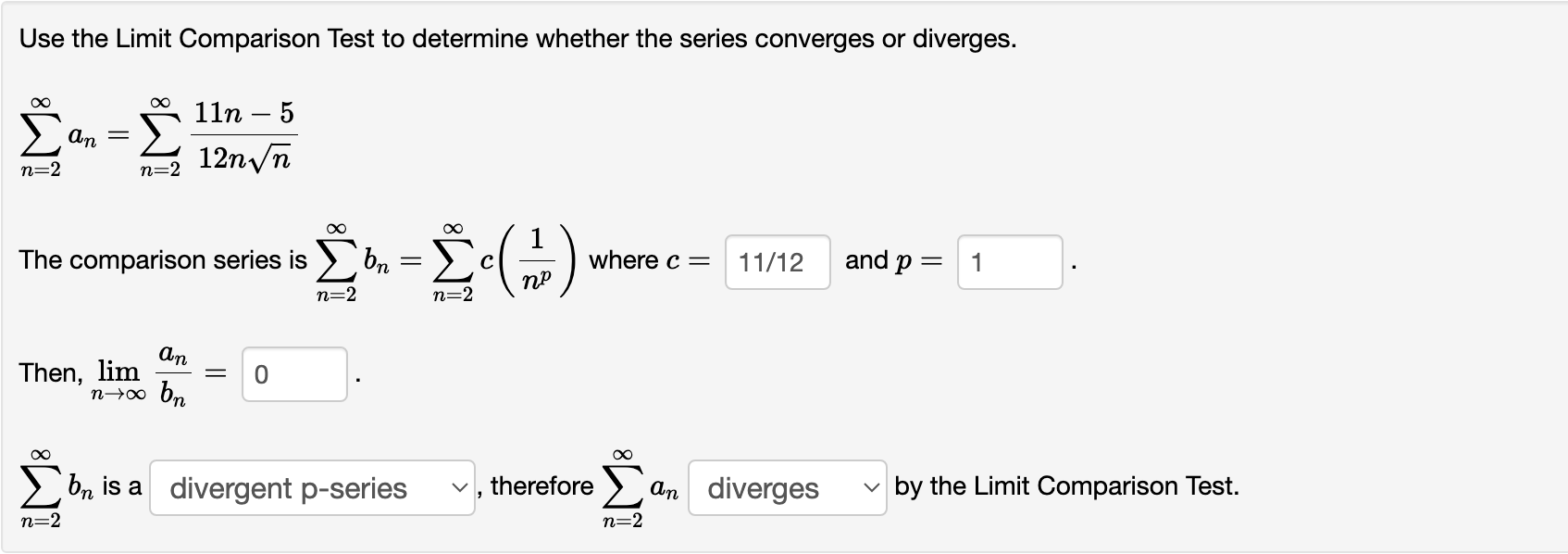
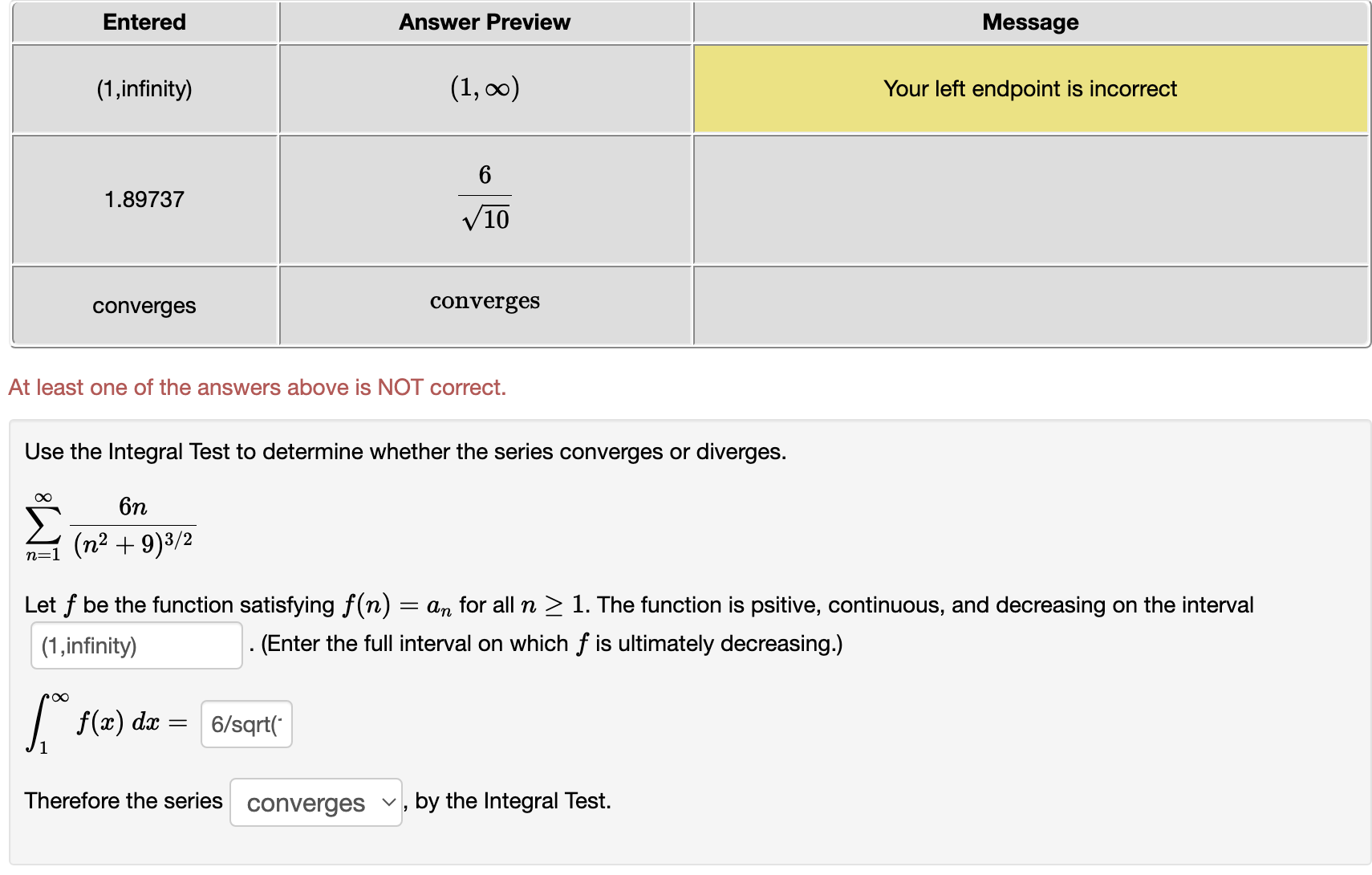
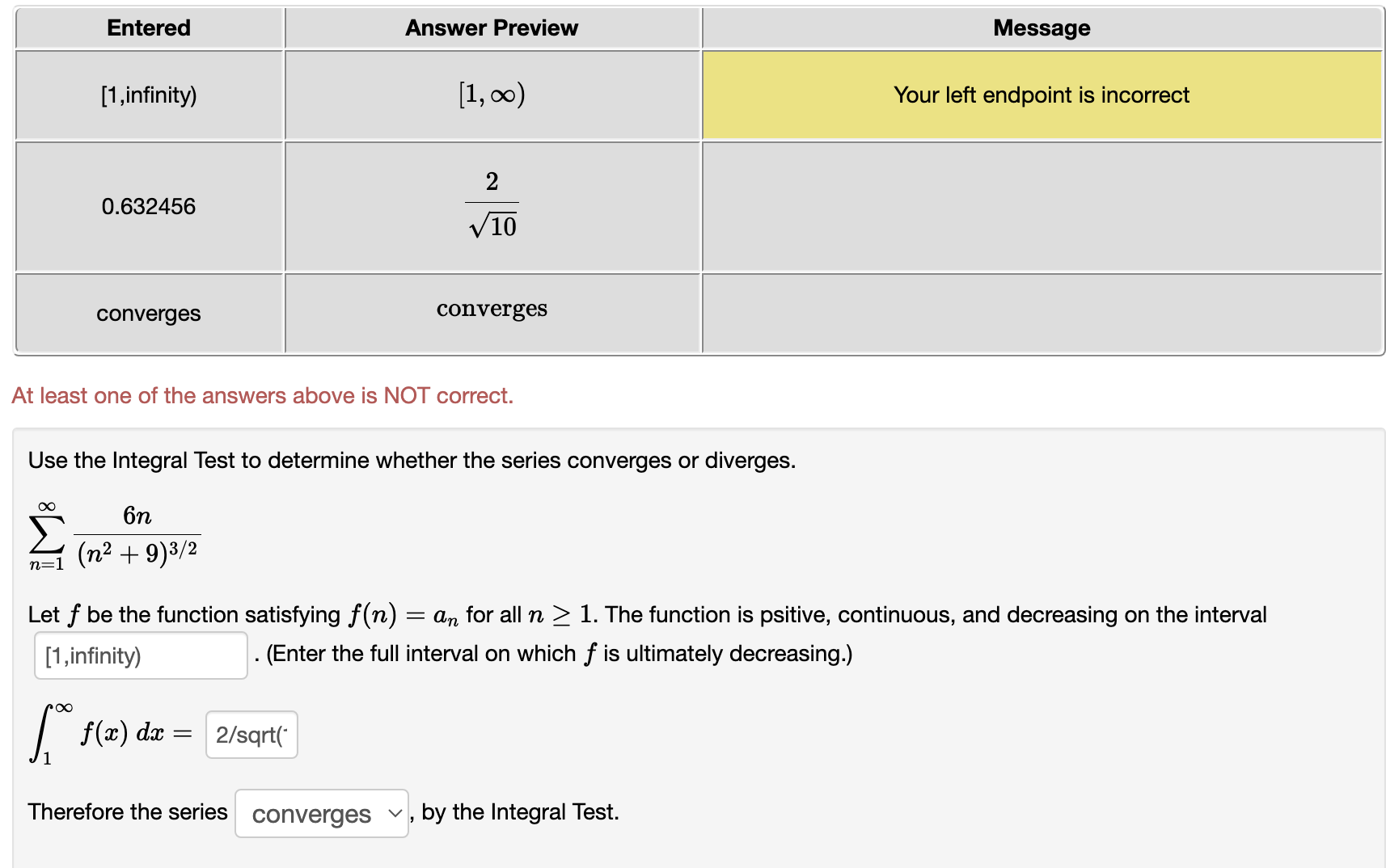
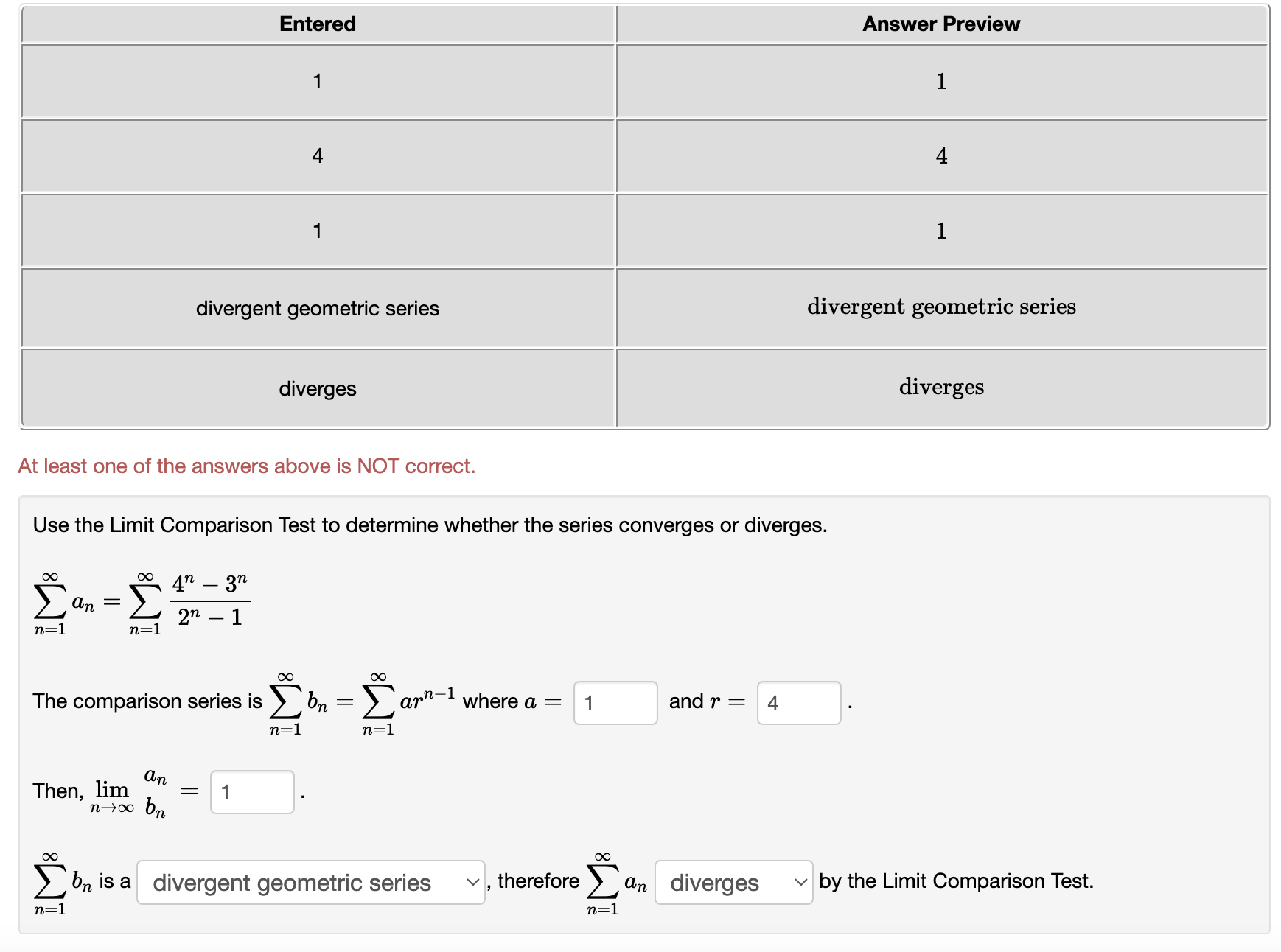
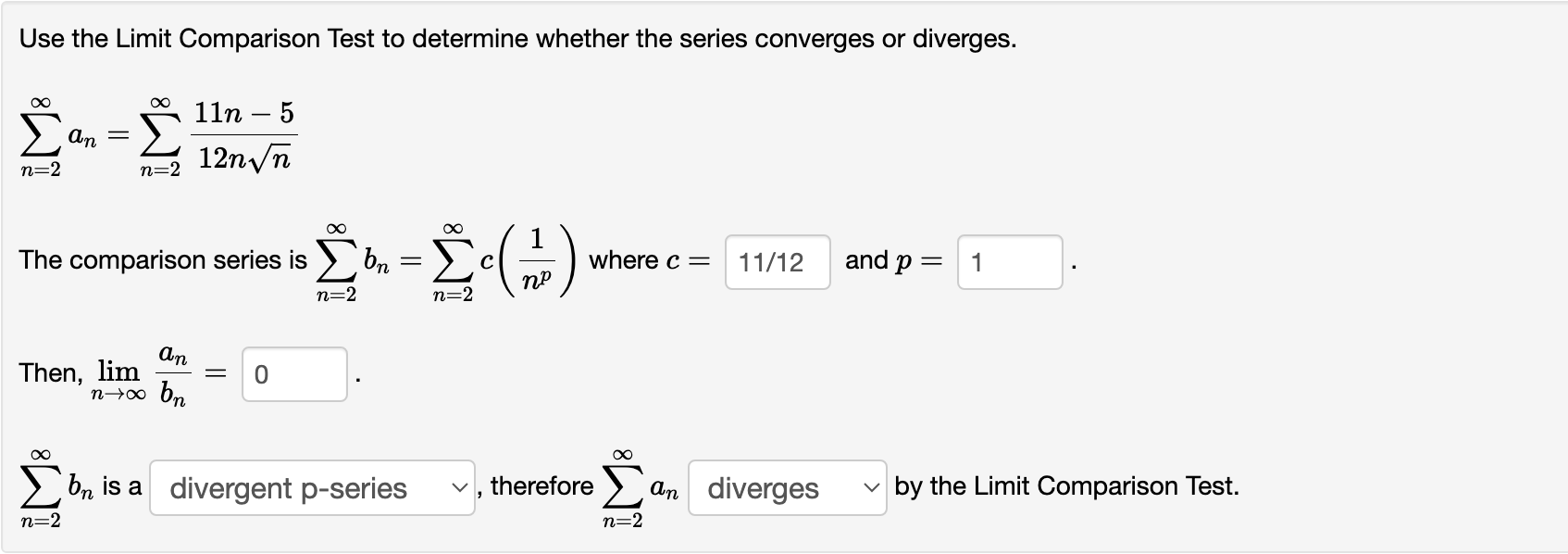
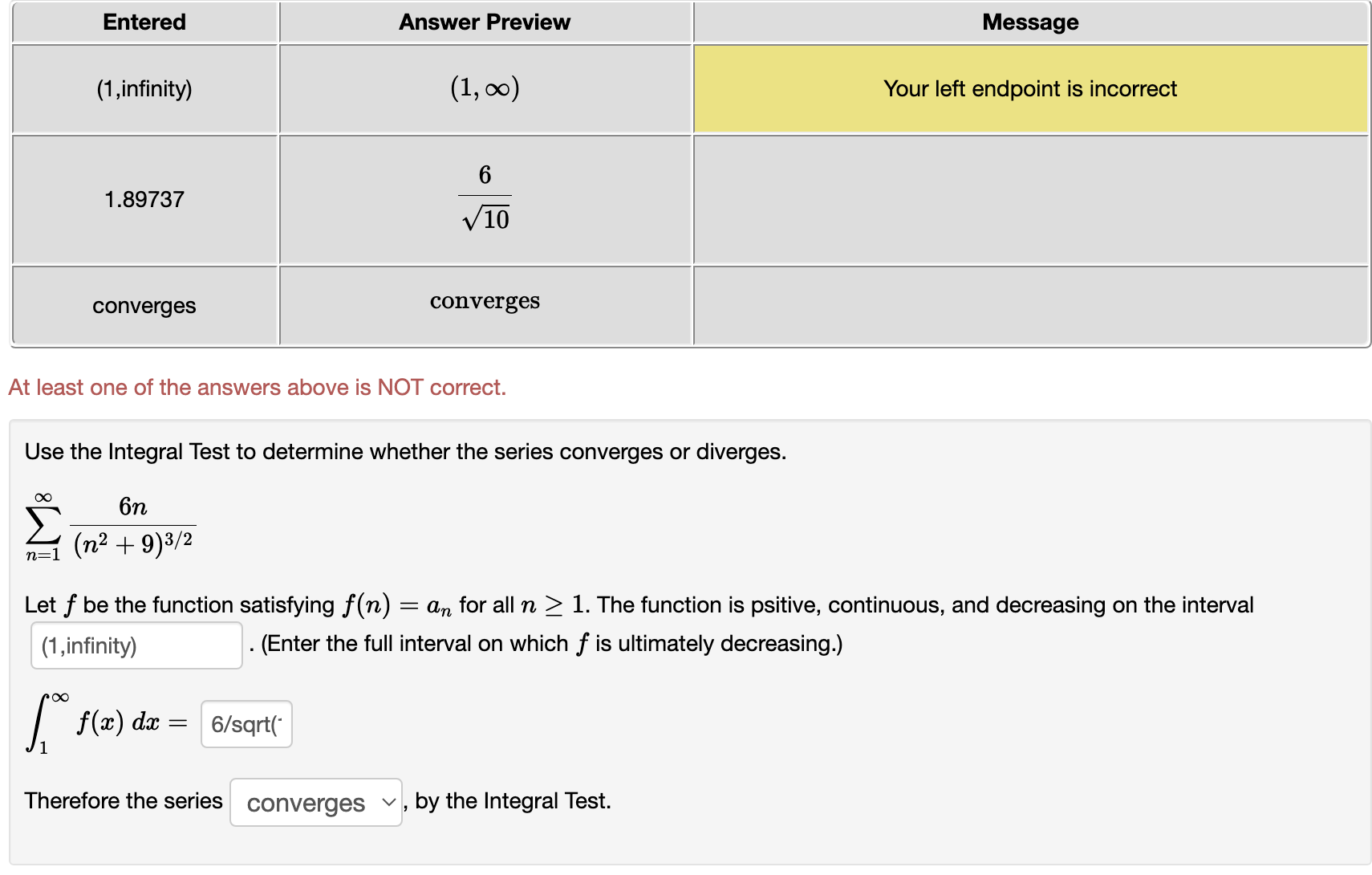
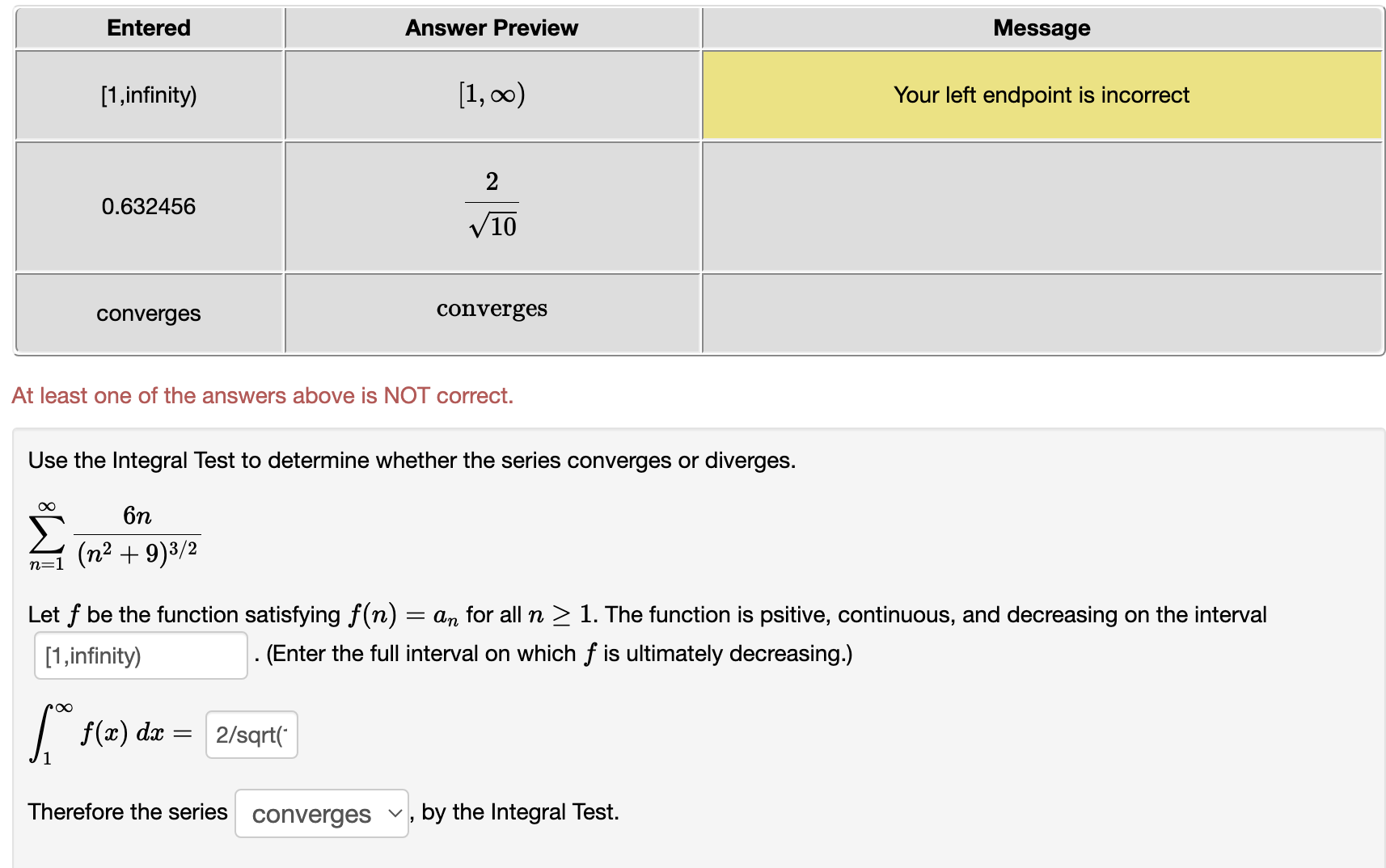
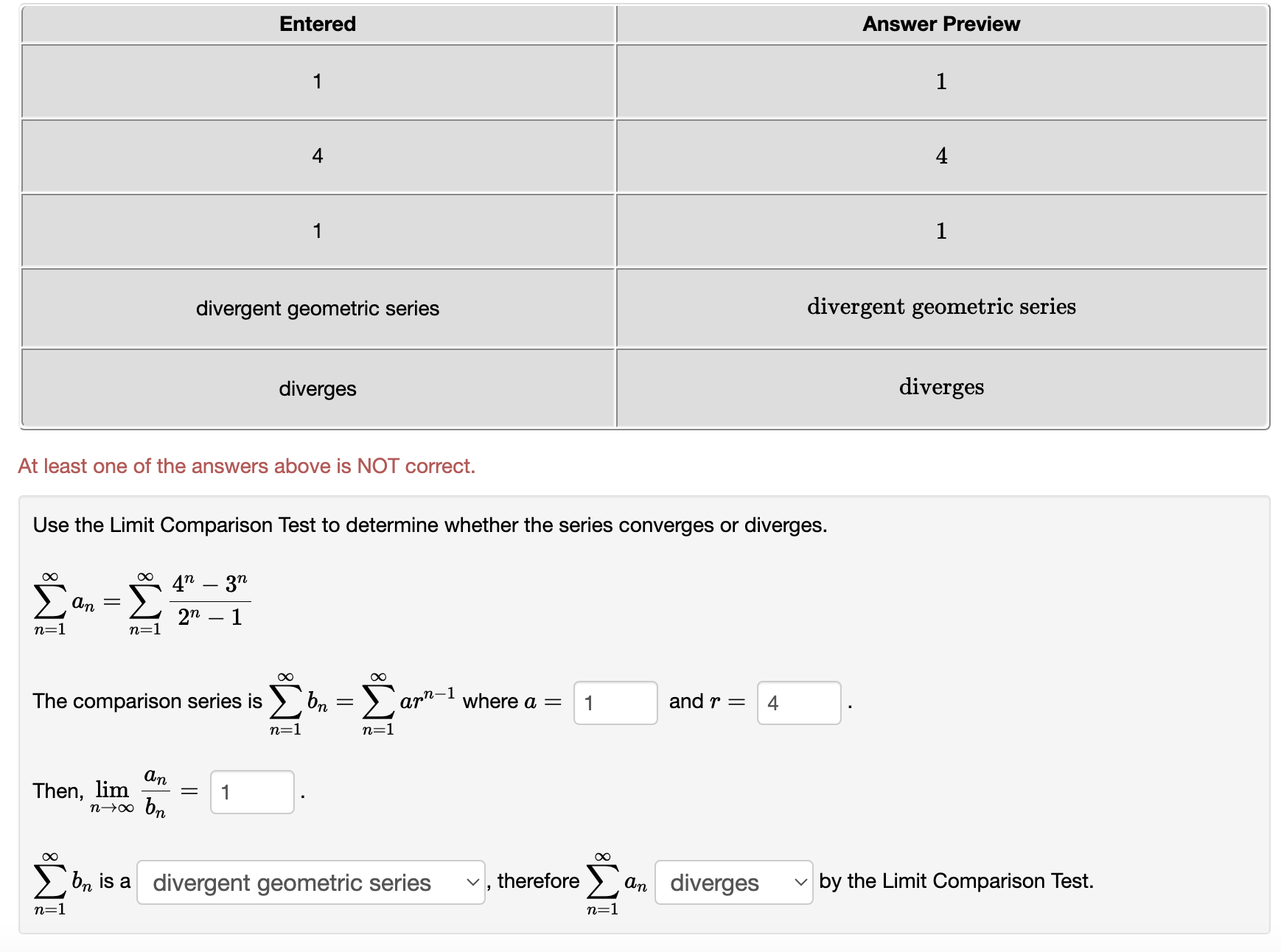
Use the Limit Comparison Test to determine whether the series converges or diverges. n _ \":1 1 + 771,3 71:1 ()0 00 1 The comparison series is 2 bn : Z C(np) where c : 8/7 and p 2 1 71:1 11:1 _ (1 Then, hm in = 0 nmo b\" 00 00 Z I)\" is a divergent pseries v , therefore Z: an diverges v by the Limit Comparison Test. 71:1 71:1 Use the Limit Comparison Test to determine whether the series converges or diverges. n22 n22 n 00 00 1 The comparison series Is 2 b\" : 26(7)?) where c : 11/12 and P I 1 n:2 n:2 (1 Then, lim n = 0 n>oo b,\" 00 00 2 bn is a divergent pSeries v , therefore Z 0.11 diverges v by the Limit Comparison Test. 11:2 11:2 Use the Limit Comparison Test to determine whether the series converges or diverges. 00 00 471 _ 3n 2\"" I Z W 71:1 11:1 ()0 ()0 The comparison series is E b = E ctr-"'1 where a = and 1' = n:1 71:1 . an Then, hm : nmo bn GO ()0 2: 611 is a ? v , therefore 2: an ? v by the Limit Comparison Test. \"=1 71:1 Use the Limit Comparison Test to determine whether the series converges or diverges. \"0 9n2 + 3n + 10 2% = Z 7 4 \":1 : 871 +671, +3n DC 00 1 The com arison series is b : c wherec: and : D Z R 2 (up) P 0, Then, lim n : mew h; 00 00 2: bn is a ? v , therefore 2 an ? v by the Limit Comparison Test. \":1 n21 Entered Answer Preview Message (1 ,infinity) (1, 00) Your left endpoint is incorrect 1 .89737 6 x/lO converges converges At least one of the answers above is NOT correct. Use the Integral Test to determine whether the series converges or diverges. i0: 6n \":1 (n2 + 9)\" Let f be the function satisfying f(n) = an for all n 2 1. The function is psitive, continuous. and decreasing on the interval (1 ,infinity) . (Enter the full interval on which 1' is ultimately decreasing.) [:0 f(m) dm = 6/sqrt(' Therefore the series converges v , by the Integral Test. Entered Answer Preview Message [1 ,infinity) [1, 00) Your left endpoint is incorrect 0.632456 2 v 10 converges converges At least one of the answers above is NOT correct. Use the Integral Test to determine whether the series converges or diverges. f: 6n \":1 (in2 + 9W2 Let f be the function satisfying f(n) : an for all n 2 1. The function is psitive, continuous, and decreasing on the interval [1 ,infinity) . (Enter the full interval on which f is ultimately decreasing.) l1 f(:i:) d3: 2/sqrt(' Therefore the series converges v . by the Integral Test. l Entered | Answer Preview 3 1 .5 2 11 0.91 6666666666667 7 12 convergent pseries convergent pseries converges converges At least one of the answers above is NOT correct. Use the Limit Comparison Test to determine whether the series converges or diverges. (X: (X: 1 The comparison series is 2 bn : Z C(np) where c = 1 and p = 3/2 11:2 n=2 0. Then, Jim in = 11/12 nmo bn 00 00 2 bn is a convergent p-59n35 v , therefore Z an converges v by the Limit Comparison Test. n=2 n=2 Entered Answer Preview 4 4 divergent geometric series divergent geometric series diverges diverges At least one of the answers above is NOT correct. Use the Limit Comparison Test to determine whether the series converges or diverges. 47 - 3n an 2n - 1 n= n=1 The comparison series is on arn- where a = 1 and r = 4 n= 1 n=1 Then, lim an L = 1 n too on bn is a divergent geometric series v, therefore an diverges v by the Limit Comparison Test. n=1 n=1Entered Answer Preview 3.5 N/ V 0 O convergent p-series convergent p-series converges converges At least one of the answers above is NOT correct. Use the Limit Comparison Test to determine whether the series converges or diverges. 18 Von2 + 3n + 10 an n=1 n= 1 8n7 + 6n4 + 3n The comparison series is > bn mp where c = 1 and p = 7/2 Then, lim an = 0 n too on Con is a convergent p-series , therefore an converges v by the Limit Comparison Test. n=1 n= 1