can someone help me with Huffman code? I have no idea how to do this one.

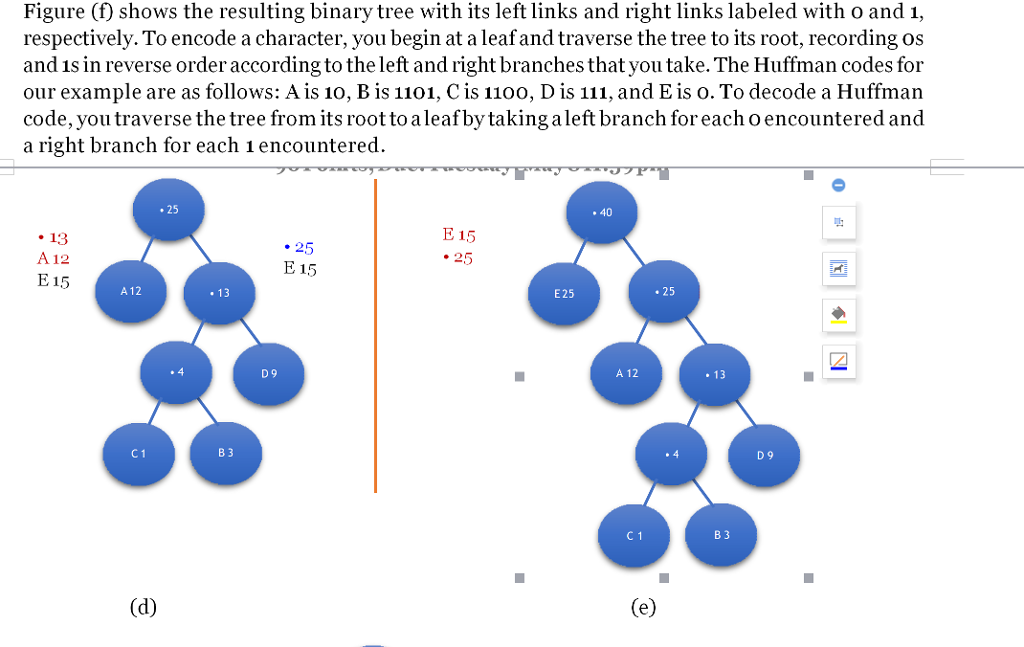
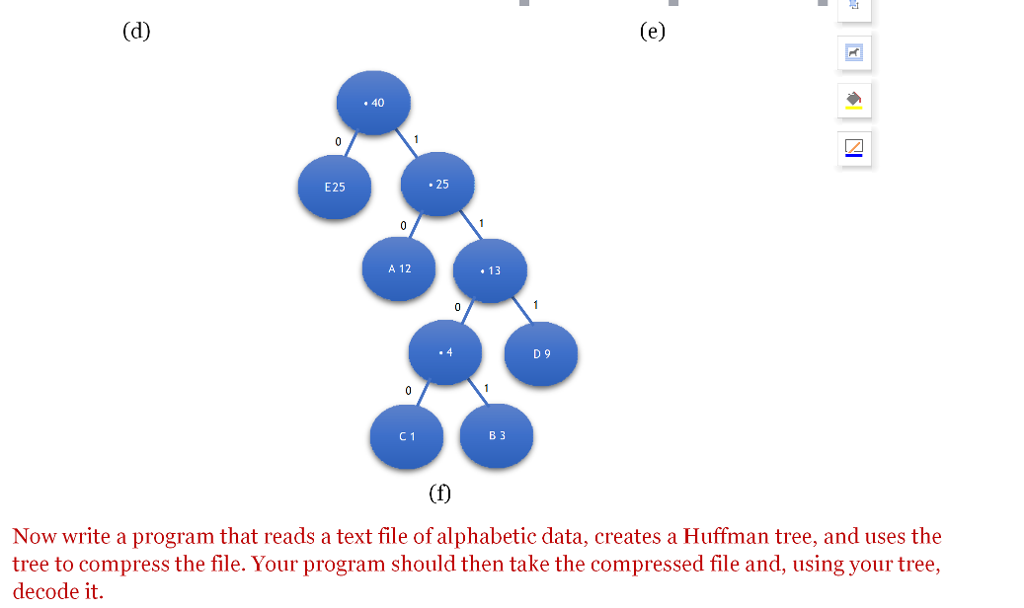
Huffman coding is a technique that compresses the size of data. For example, a .zip file of a text documentis a compressed version ofthe original document.Thisso-calledloseless data compression is a result Huffman coding. Although ASCII and Unicode use bit strings having a fixed length-8 and 16, respectively-to represent symbols, Huffman codes have variable lengths. These codes are based on the frequency of occurrences of a symbol in a given data set. Symbols that occur frequently have shorter codes tharn those occurring less frequently. A binary tree-called a Huffman tree-is used to generate these codes. For example, let's encode some text composed of only of letters A through E. Suppose these letters occur with the following frequencies: A, 12 times; B, 3 times; C, 1time; D, 9 times; and E, 15 times. We need to arrange these letters bytheir frequencies in increasing order. To do so, we associate each letterwith its frequency of occurrences and add these pairs to a collection, such as a sorted list or a priority queue. The result is shown in the Figure (a). Now we remove the two entries having the lowest frequencies and make them leaves in a binary tree. The parent of these leaves is a node containing the sum ofthe frequencies in the leaves as illustrated in Figure (b). Since the parent contains only a frequency, the letter portion ofthe node is null, which is shown as. in the figure. We now add the contents of the parent to our list or queue, as shown to the right of the tree in Figure (b). When we remove the next two entries from the list, we create a new leaf containing D 9 and join it to the existing tree with a new root containing the sim of the frequencies in its two children. The result is given in Figure (c). Note that we then place the contents of this new root in tis correct orderwithin the remaining data. Figure (d) and (e) showthe remaining steps in this process. 4 3 A 12 12 D 9 Huffman coding is a technique that compresses the size of data. For example, a .zip file of a text documentis a compressed version ofthe original document.Thisso-calledloseless data compression is a result Huffman coding. Although ASCII and Unicode use bit strings having a fixed length-8 and 16, respectively-to represent symbols, Huffman codes have variable lengths. These codes are based on the frequency of occurrences of a symbol in a given data set. Symbols that occur frequently have shorter codes tharn those occurring less frequently. A binary tree-called a Huffman tree-is used to generate these codes. For example, let's encode some text composed of only of letters A through E. Suppose these letters occur with the following frequencies: A, 12 times; B, 3 times; C, 1time; D, 9 times; and E, 15 times. We need to arrange these letters bytheir frequencies in increasing order. To do so, we associate each letterwith its frequency of occurrences and add these pairs to a collection, such as a sorted list or a priority queue. The result is shown in the Figure (a). Now we remove the two entries having the lowest frequencies and make them leaves in a binary tree. The parent of these leaves is a node containing the sum ofthe frequencies in the leaves as illustrated in Figure (b). Since the parent contains only a frequency, the letter portion ofthe node is null, which is shown as. in the figure. We now add the contents of the parent to our list or queue, as shown to the right of the tree in Figure (b). When we remove the next two entries from the list, we create a new leaf containing D 9 and join it to the existing tree with a new root containing the sim of the frequencies in its two children. The result is given in Figure (c). Note that we then place the contents of this new root in tis correct orderwithin the remaining data. Figure (d) and (e) showthe remaining steps in this process. 4 3 A 12 12 D 9