can someone help please?

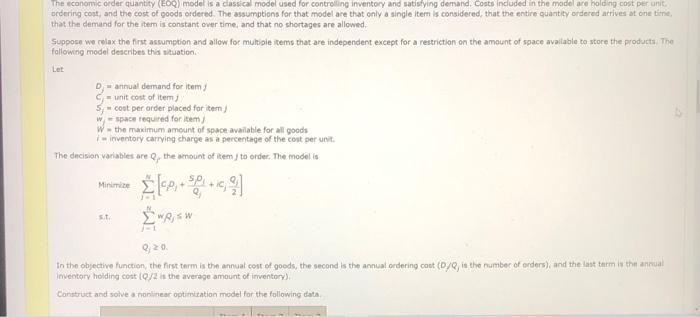
The economic order quantity (EOQ) mode is a classical model used for controling inventory and satisfying demand, costs incuded in the model are holding cost per untic. brdering cort, and the cost of goods ordered. The assumptions for that model are that only a single item is considered, that the entire quastity ordered arrives at one time, that the demand for the item is constant over time, and that no shortages are allowed. Suppose we relax the fins assumption and allow for multipie items that are independent except for a restriction on the amount of space available to store the products. The following model deseribes this situation. Let Dj=annualdemandforitemfcj=unitcostofitemj5j=costperorderplacedforitemjwj=spacerequiredforitemjW=themaximumameuntofspwceavailableforallgoodsi=inventorycarryingchargeasapercentageofthecostperunit. The decisian variables are Qf, the amount of item J to order. The model is Minitizes.t.j=1N[ciDj+Qj5Dij=1NNiwQjwQj0. In the objective function, the first term is the annual cost of goeds, the second is the annual ordering cast (D/Q, is the number of orders), and the last thrm is thit annual inventory holding cost (Q/2 is the average amount of irventory). Conatruct and solve a nonlinear optimitation model for the fallowing data. Complete the model Min[()2,000+Q1((0,000)+0.30()+2Q1 +50()+Q2((,000)+0.30()2Q2 +()1,000+((Q3(0.000)+0.30()2Q3] [(Qj)Q2,Q30. )=Q2+()Q3]9,000 Solve the model. (Round Q1,Q2, and Q1 to three decimal places and total cost (in \$) to two decimal places.) Q1=Q2=Q3= Total cost =$ The economic order quantity (EOQ) mode is a classical model used for controling inventory and satisfying demand, costs incuded in the model are holding cost per untic. brdering cort, and the cost of goods ordered. The assumptions for that model are that only a single item is considered, that the entire quastity ordered arrives at one time, that the demand for the item is constant over time, and that no shortages are allowed. Suppose we relax the fins assumption and allow for multipie items that are independent except for a restriction on the amount of space available to store the products. The following model deseribes this situation. Let Dj=annualdemandforitemfcj=unitcostofitemj5j=costperorderplacedforitemjwj=spacerequiredforitemjW=themaximumameuntofspwceavailableforallgoodsi=inventorycarryingchargeasapercentageofthecostperunit. The decisian variables are Qf, the amount of item J to order. The model is Minitizes.t.j=1N[ciDj+Qj5Dij=1NNiwQjwQj0. In the objective function, the first term is the annual cost of goeds, the second is the annual ordering cast (D/Q, is the number of orders), and the last thrm is thit annual inventory holding cost (Q/2 is the average amount of irventory). Conatruct and solve a nonlinear optimitation model for the fallowing data. Complete the model Min[()2,000+Q1((0,000)+0.30()+2Q1 +50()+Q2((,000)+0.30()2Q2 +()1,000+((Q3(0.000)+0.30()2Q3] [(Qj)Q2,Q30. )=Q2+()Q3]9,000 Solve the model. (Round Q1,Q2, and Q1 to three decimal places and total cost (in \$) to two decimal places.) Q1=Q2=Q3= Total cost =$