can someone please explain the excel formulas in the excel graph at the bottom of this question ?

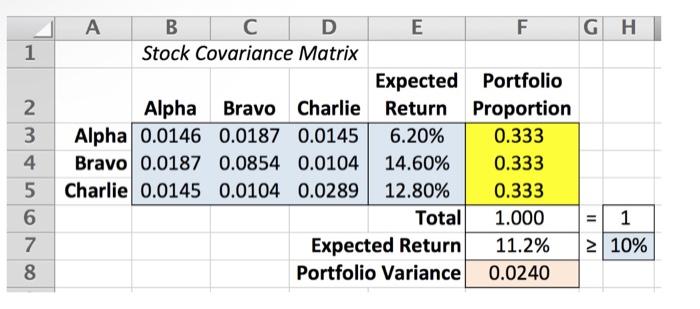
herevel that the expected teturn of the pertille in tant? Rxplain? Qoestion 9: Ideatify the varialles, ebejectives, and cunotrainks in thes peublem. (Hith, diviles the pertilio mysuly ameas the 3 atiolik Question le: Is the soluriten shown mbeen Jawaz WTy ar =hy nive? Explain. not know if Solver has bewe run bo eltalin an egtimal moliution). How dlo you kmew it QN1>030 Markowitt showed that the evpected return of the portfollo is Butiding a Furtfollis aptimization Bedtel - 5tock Selection E=0.062xy+0.146xy+0.128xy Stock Selection case study Markowitz won the Nobel Drize for his werk in stock portfolio theory. Me was the Ant to measure portfolie riak using the yarlance of returns.' He lntroduced stock selection based on an "efficlent frontier". namely, by picking the stocks that give the portfole "with minimum variance for a given return" and "masimum cetion for a given variance." An invester is conpldering buping a cembinatien of 3 stecks - "Alpad, "Mravo," and "Charle"+ using Marhewitr's pertfolio optimizatien methed. The expected returns and risk of these toeks are piven in Table 1 . Tashe 1. Meturn and anisk tbata for 3 stecks An invester would lik to purthase obree combination st the 3 socko te build a pertolis that gireb at leant a 1044 return at the lowest possibie risk ch.t. at minimam gertiota variance). A portholo' variasce fepends os hoe each indidual itedk'e price fuctuations are correlated with every other ateck's. kneme as the cevariance of returns. The covariances are ghen in the varlance covariance matris in Tatble 2. For example, the covariance between Atgha and Eravo is 0.0197. Table 2. Variance covariance Aatris ef Meturms Accerding to Markowitz, if xy,xy and x, is the proportion of the portolos invested in Alpha, Bravo, and Charlie, respectively, then x1+x2+x1=1. QN1>030 Markowitt showed that the evpected return of the portfollo is Butiding a Furtfollis aptimization Bedtel - 5tock Selection E=0.062xy+0.146xy+0.128xy Stock Selection case study Markowitz won the Nobel Drize for his werk in stock portfolio theory. Me was the Ant to measure portfolie riak using the yarlance of returns.' He lntroduced stock selection based on an "efficlent frontier". namely, by picking the stocks that give the portfole "with minimum variance for a given return" and "masimum cetion for a given variance." An invester is conpldering buping a cembinatien of 3 stecks - "Alpad, "Mravo," and "Charle"+ using Marhewitr's pertfolio optimizatien methed. The expected returns and risk of these toeks are piven in Table 1 . Tashe 1. Meturn and anisk tbata for 3 stecks An invester would lik to purthase obree combination st the 3 socko te build a pertolis that gireb at leant a 1044 return at the lowest possibie risk ch.t. at minimam gertiota variance). A portholo' variasce fepends os hoe each indidual itedk'e price fuctuations are correlated with every other ateck's. kneme as the cevariance of returns. The covariances are ghen in the varlance covariance matris in Tatble 2. For example, the covariance between Atgha and Eravo is 0.0197. Table 2. Variance covariance Aatris ef Meturms Accerding to Markowitz, if xy,xy and x, is the proportion of the portolos invested in Alpha, Bravo, and Charlie, respectively, then x1+x2+x1=1. Questuths of to is rejer to the pouenung poryjono seicction probern. Markowitz won the Nobel Prize for his work in stock portfolio theory; be was the first to measure portfolio risk using the variance of returns." He introduced stock seloction besed on an -effichent frontier," namely, by picking the stocks that give the portfolio "with minimam variance for a given returu" and "maximum return for a given variance." An investor is considering buying a combination of 3 stocks - "Alpha," "Bravo," and "Charlie" - ming Markowitz's portfolio optimization method. The expected retums and risk of these stocks are given in Table 2. An investor would like to purchase some combination of the 3 stocks to build a portfolio that gives at lesst a 10% return at the lowest possible risk (i.e. at minimum portfolio variance). A portfolio's variance depends on how each individual stock's price flactuations are correlated with every other 1 His seminal paper is H.M. Markowitz, 1952, "Portfolio Seloctich," Journal of Finmen, T(1), T-91. 2 ibid, p. 82 . stock's, known as the covariance of returns, and so she identified the covariances given in Table 3. For example, the covariance betwoen Alpha and Bravo is 0.0187.3 She recalled that according to Markowitz, she should let x1,x2, and x3 be the proportion of the portfolio invested in Alphn, Bravo, and Charlie, respectively, with x1+x2+x3=1. Marlowitz showed that the expected return of the portfolio is E=0.062x1+0.146x2+0.128x3 Similarly, Markowitz showprl that the portfolio's varianco is the following function of eowarianes: V=.0146x1x1+.0187x1x2+.0145x1x3+.0187x2x1+.0854x2x2+.0104x2x3+.0145x3x1+.0104x3x2+.0289x3x3