Can someone please solve this.

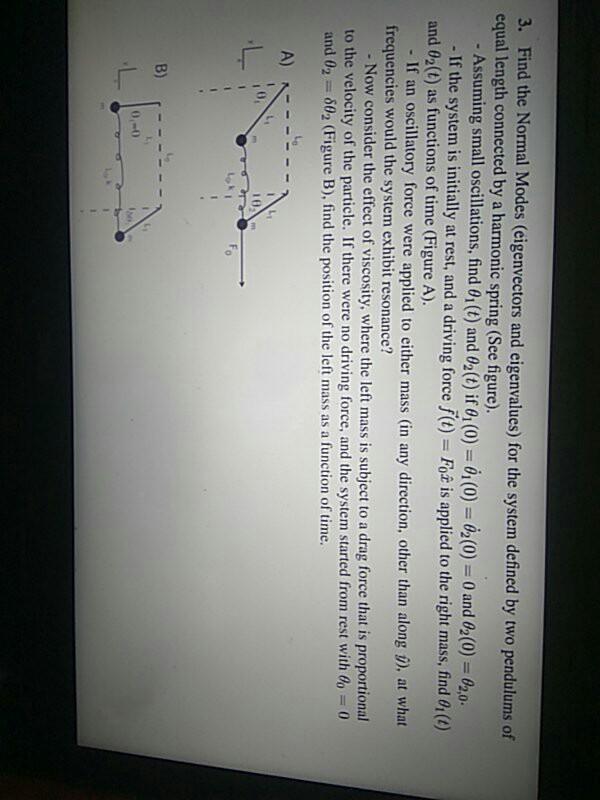
3. Find the Normal Modes (eigenvectors and eigenvalues) for the system defined by two pendulums of equal length connected by a harmonic spring (See figure). - Assuming small oscillations, find 0(t) and 02(t) if 0 (0) = 0 (0) = 02(0) = 0 and 02(0) = 02,0- -If the system is initially at rest, and a driving force f(t) = Foi is applied to the right mass, find 01 (6) and 02(t) as functions of time (Figure A). If an oscillatory force were applied to either mass (in any direction, other than along 9), at what frequencies would the system exhibit resonance? - Now consider the effect of viscosity, where the left mass is subject to a drag force that is proportional to the velocity of the particle. If there were no driving force, and the system started from rest with 0o = 0 and 02 = 50, (Figure B), find the position of the left mass as a function of time. A) B) 3. Find the Normal Modes (eigenvectors and eigenvalues) for the system defined by two pendulums of equal length connected by a harmonic spring (See figure). - Assuming small oscillations, find 0(t) and 02(t) if 0 (0) = 0 (0) = 02(0) = 0 and 02(0) = 02,0- -If the system is initially at rest, and a driving force f(t) = Foi is applied to the right mass, find 01 (6) and 02(t) as functions of time (Figure A). If an oscillatory force were applied to either mass (in any direction, other than along 9), at what frequencies would the system exhibit resonance? - Now consider the effect of viscosity, where the left mass is subject to a drag force that is proportional to the velocity of the particle. If there were no driving force, and the system started from rest with 0o = 0 and 02 = 50, (Figure B), find the position of the left mass as a function of time. A) B)