Can someone provide a solution using mathematical writing (Complete English Sentences) for the following questions.

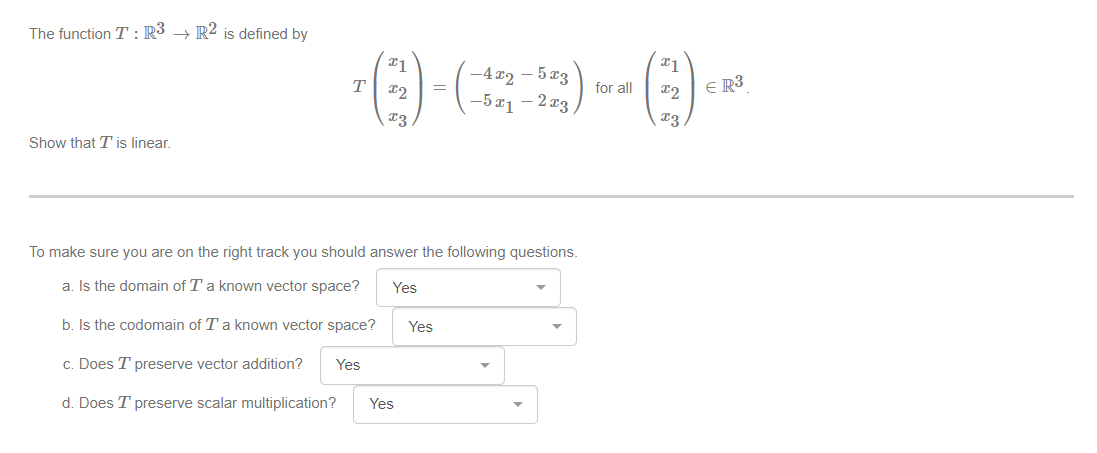
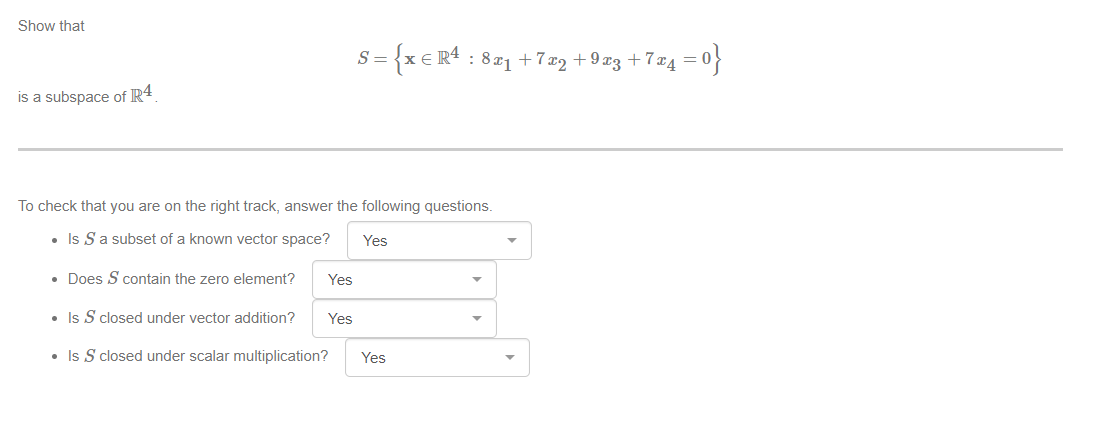
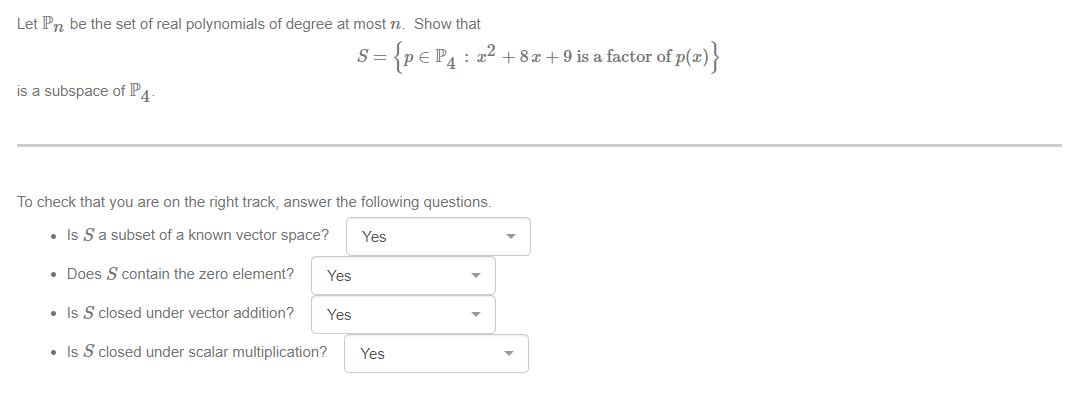
The function T : R3 3~ R2 is dened by Show that T is linear. To make sure you are on the right track you should answer the following questions. a. Is the domain of T a known vector space? b. Is the codomain of T a known vector space? c. Does T preserve vector addion? d. Does T preserve scalar multiplication? Showthat 8: {I E R4 2331 +722 +933 +724 =0} is a subspace of R4. To check that you are on the right track, answer the following questions. o Is S a subset of a known vector space? . Does S contain the zero element? o Is S closed under vector addition? . ls S closed under scalar multiplication? Let JP\" be the set of real polynomials of degree at most 73. Show that S: {pEP4 : 22 +83+Qisafactorofp{:c)} is a subspace of P4. To check that you are on the right track, answer the following questions. . ls S a subset of a known vector space? 0 Does 8 contain the zero element? o Is S closed under vector addition? o Is S closed under scalar multiplication? Consider the suspension bridge shown below, where there are two main cables, hangers, and the deck. The bridge is 20 meters long. The self-weight of the deck and any loads applied on the deck (such as people standing on this bridge) is transferred to the cables through the hangers. Figure 1: Sketch of a. suspension bridge. Setup a Cartesian coordinate system to model one of the main cables with the lowest point of this cable intersecting the vertical axis at height 5 meters. The distributed load (self-weight of the deck and loads applied on the deck supported by that cable) is described by a function w(:c) and it is measured in Newtons per meter (Nim). The resultant force W (3:) is given by W(a:] = sz(u)d. and it is measured in Newtons (N). The shape of the cable is given by a function y (3) whose derivative with respect to m, the horizontal distance from the lowest point, is given by the ratio of the resultant force and H, the tension in the cable at the lowest point measured in Newtons. Here y and .7: represent respectively the vertical and horizontal axis. a) Write down the differential equation that describes the shape of the cable in terms of W(:::) and H. b) We are given that the function y is even, so we may assume .1: 2 0. Hence, suppose that for :1: in [0, 10], the distributed load is l approximated by the function W(:c) = (3 + at) 9 {where we have implicitly multiplied by a constant to ensure that the units of W (2:) are Newtons), and that the tension H at the lowest point of the cable is 55, 112 N (Newtons). Write down what you can say about the differential equation you found in part (a) and motivate your claims: what is the order? Is it linear? What method best applies to solve this equation? What is the domain of a solution expected to be? c} Hence, given the initial condition embedded in the wording of the problem, solve the differential equation by writing down all the steps and their justications when needed. (In order to nd the ght initial condition, read the question again from the beginning: when a: = U, y 2?) d) What is the value of y at :1: = 6 m? (Correct to exactly 5 signicant gures.)