can u use jupyter notes book python code to solve the question ?

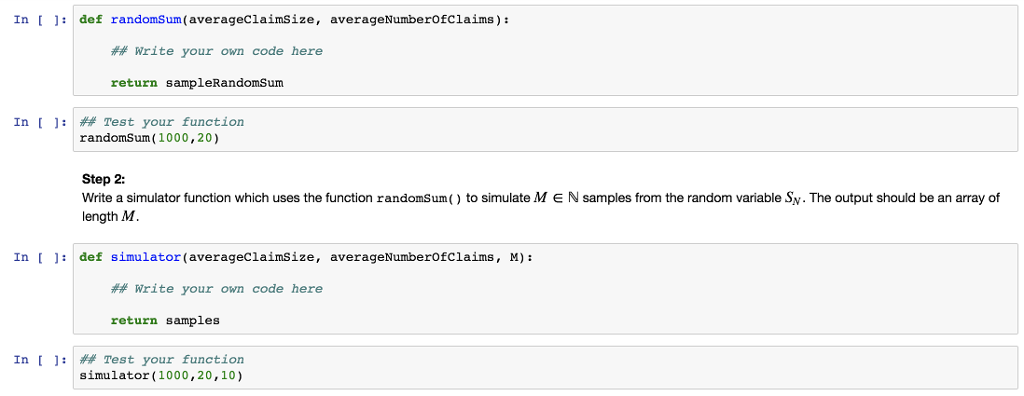
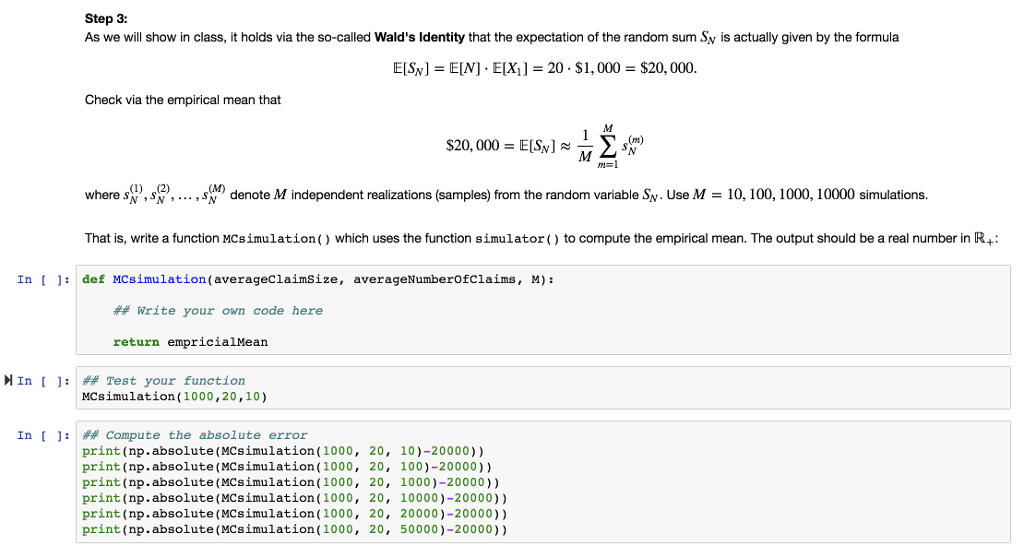
A stochastic model for a car insurance company's total cost of damages from traffic accidents goes back to the work by Van der Lann and Louter, "A statistical model for the costs of passenger car traffic accidents", Journal of the Royal Statistical Society (1986). For every k = 2, 3 we denote by the random variable Xk the US dollar amount of a damage from a policy holders t affic accident which will occur during the year 2019. We assume that X1, X2 is an i.i.d. (independent and identically distributed) sequence of exponentially distributed random variables with an average claim size of 1,000USD. The(random)totalnumberofaccidentsN$ in 2019 is expected to be Poisson distributed with 20 claims on average It is assumed that the number of accidents is independent of the US dollar amount of damages for each accident. That is, the random variable N is independent of the random variables X1,X2. The total costs for the insurance company by the end of 2019 will thus be given by the random sum k=1 Note that the total number N of accidents is random! A stochastic model for a car insurance company's total cost of damages from traffic accidents goes back to the work by Van der Lann and Louter, "A statistical model for the costs of passenger car traffic accidents", Journal of the Royal Statistical Society (1986). For every k = 2, 3 we denote by the random variable Xk the US dollar amount of a damage from a policy holders t affic accident which will occur during the year 2019. We assume that X1, X2 is an i.i.d. (independent and identically distributed) sequence of exponentially distributed random variables with an average claim size of 1,000USD. The(random)totalnumberofaccidentsN$ in 2019 is expected to be Poisson distributed with 20 claims on average It is assumed that the number of accidents is independent of the US dollar amount of damages for each accident. That is, the random variable N is independent of the random variables X1,X2. The total costs for the insurance company by the end of 2019 will thus be given by the random sum k=1 Note that the total number N of accidents is random