Can you answer these 2problems?

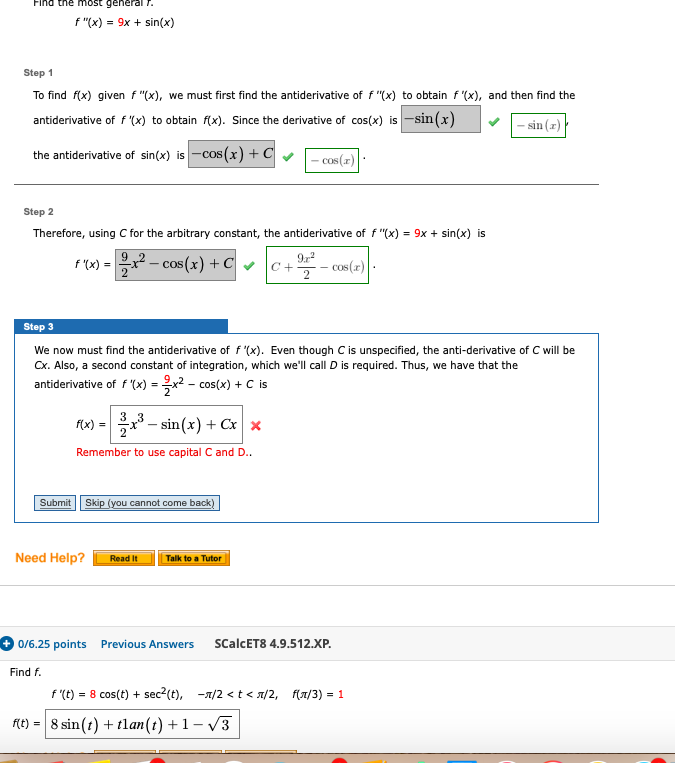
Find the most general r f "(x) = 9x + sin(x) Step 1 To find f(x) given f"(x), we must first find the antiderivative of f "(x) to obtain f'(x), and then find the antiderivative of f '(x) to obtain f(x). Since the derivative of cos(x) is-sin(x) - sin (r) the antiderivative of sin(x) is-cos(x) + C Step 2 Therefore, using C for the arbitrary constant, the antiderivative of f "(x) = 9x + sin(x) is F'(x)=x-cos(x) + C f(x)=x - sin(x) + Cx * Remember to use capital C and D.. Step 3 We now must find the antiderivative of f '(x). Even though C is unspecified, the anti-derivative of C will be Cx. Also, a second constant of integration, which we'll call D is required. Thus, we have that the antiderivative of f '(x) = 2x - cos(x) + C is Submit Skip (you cannot come back) Need Help? Read It -cos(x) Talk to a Tutor 9.7 C+ -cos(x). 2 0/6.25 points Previous Answers SCalcET8 4.9.512.XP. Find f. f(t) = 8 sin(t) + tlan(t) +1-3 f '(t) = 8 cos(t) + sec(t), -a/2