can you help with this proofs (algebra) question. i need help with question 3. (q3)

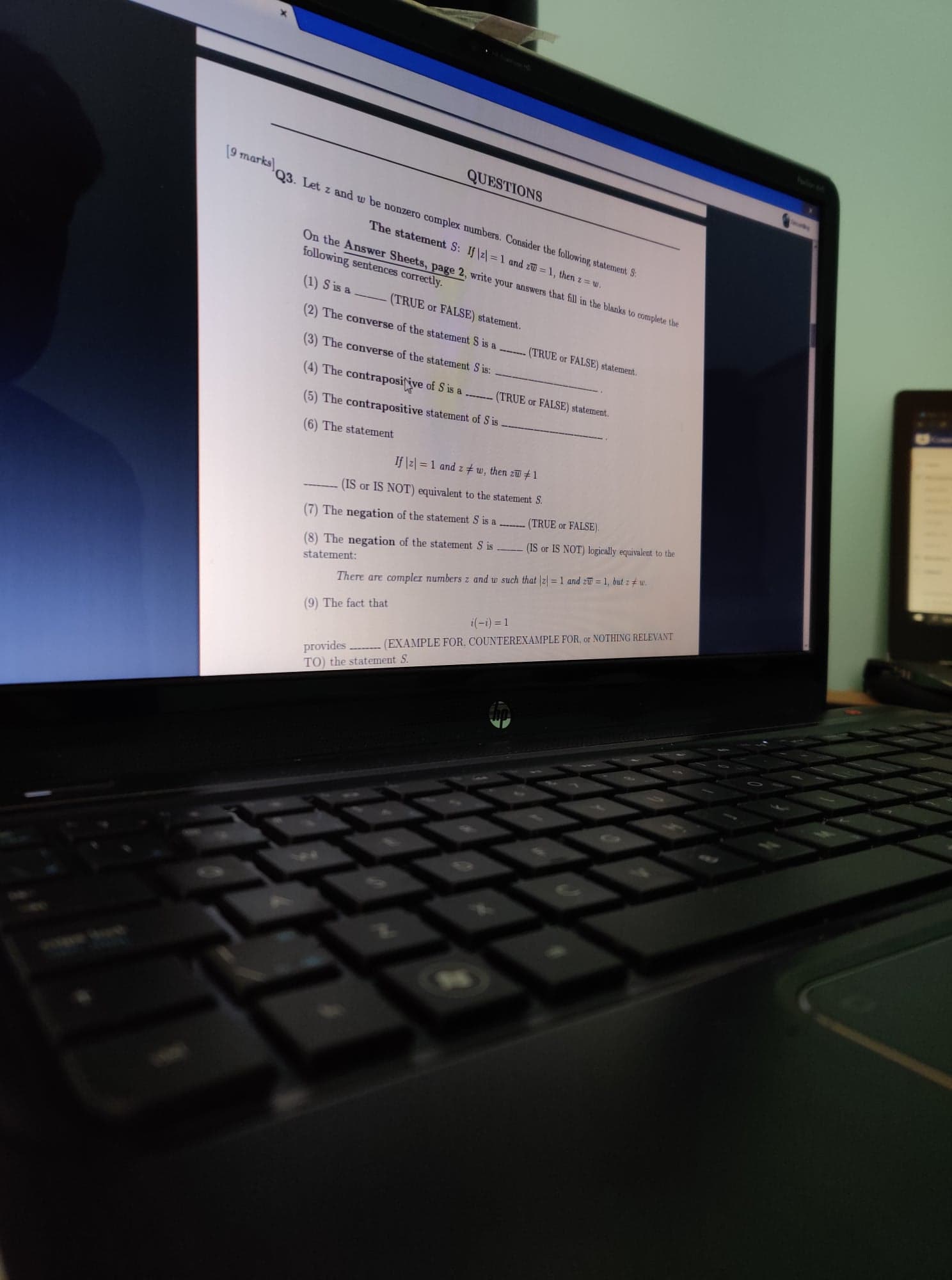
[9 marks QUESTIONS Q3. Let z and w be nonzero complex numbers. Consider the following statement S: The statement S: If (z) = 1 and zu = 1, then z = w. On the Answer Sheets, page 2, write your answers that fill in the blanks to complete the following sentences correctly. (1) Sis a _ (TRUE or FALSE) statement. (2) The converse of the statement S is a (TRUE or FALSE) statement. (3) The converse of the statement S is: (4) The contrapositive of S is a .. -- (TRUE or FALSE) statement. 5) The contrapositive statement of S is (6) The statement If |z) = 1 and z # w, then zw # 1 (IS or IS NOT) equivalent to the statement S. (7) The negation of the statement S is a .. (TRUE or FALSE). -- (IS or IS NOT) logically equivalent to the (8) The negation of the statement S is statement: There are compler numbers z and w such that (z) = 1 and aw = 1, but z # w. (9) The fact that i(-1) =1 provides _. (EXAMPLE FOR, COUNTEREXAMPLE FOR, or NOTHING RELEVANT TO) the statement S