Can you please help me with Section 3.7: 28, 37, 52, 72, and 73. Thanks so much!! :)

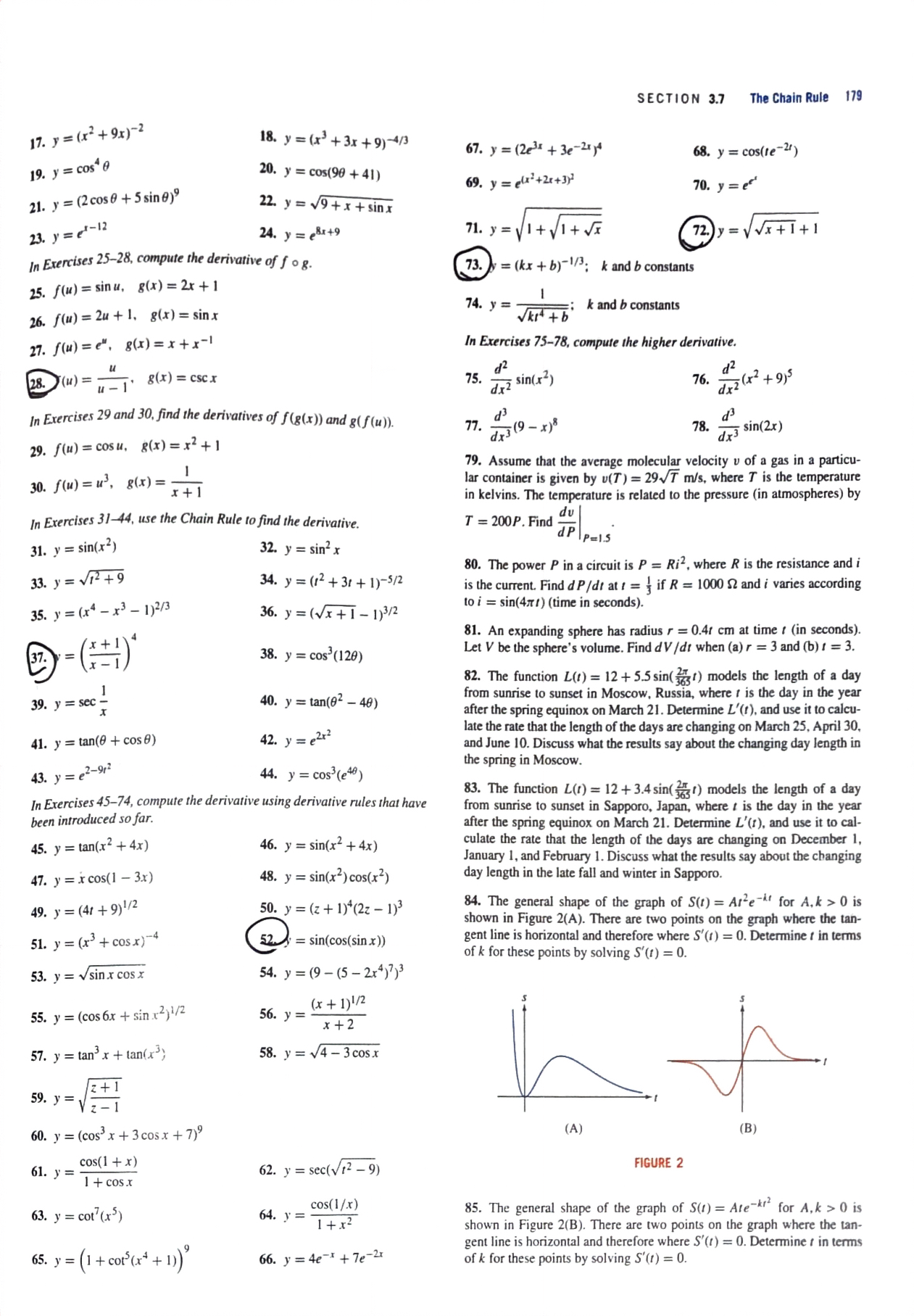
SECTION 3.7 The Chain Rule 179 17. y = (x +9x)-2 18. y = (x)+ 3x + 9)-4/3 67. y = (203 + 3e-20 ) 68. y = cos(te-2) 19. y = cos 0 20. y = cos(90 + 41) 69. y = ('+21+3) 70. y = e 21. y = (2 cos 0 + 5 sin 8) 22. y = v9 + x + sinx 23. y= e-12 24. y = (8x+9 71. y = VI+ VI+ VI 72. = VVI+ 1+1 In Exercises 25-28, compute the derivative of fog. 73. = (kx + b)-1/3: k and b constants 25. f(u) = sinu. 8(x) = 2x + 1 26. f(u) = 2u + 1. 8(x) = sinx 74. y = - Vkit + b k and b constants 27. f(u) = (", 8(x)=x+ x-1 In Exercises 75-78, compute the higher derivative. 28. (U) = - 8(x) = csc.x 75. d2 diz sin(x?) 76. dri ( * + 9)5 In Exercises 29 and 30, find the derivatives of f(g(x)) and g(f (u)). 77. - 73 (9-x) 8 78. dx3 sin(2x) 29. f(u) = cosu. 8(x) = x2 + 1 79. Assume that the average molecular velocity u of a gas in a particu- 30. f (u) = u', 8(x) = = *+ 1 lar container is given by u(T) = 29VT m/s, where T is the temperature in kelvins. The temperature is related to the pressure (in atmospheres) by In Exercises 31-44, use the Chain Rule to find the derivative. T = 200p. Find ap pel.5 du 31. y = sin(x?) 32. y = sin x 80. The power P in a circuit is P = Riz, where R is the resistance and i 33. y = Viz + 9 34. y = (12 + 31 + 1)-5/2 is the current. Find d P/dt att = if R = 1000 $2 and i varies according 35. y = (x4 - x3 - 1)2/3 36. y = (Vx + 1 - 1)3/2 to i = sin(4x/) (time in seconds). 81. An expanding sphere has radius r = 0.4r cm at time : (in seconds). 37. = (1) 38. y = cos (120) Let V be the sphere's volume. Find d V /di when (a) r = 3 and (b) 1 = 3. 82. The function L(1) = 12 + 5.5 sin( 365() models the length of a day 39. y = sec - 40. y = tan(02 - 40) from sunrise to sunset in Moscow, Russia, where / is the day in the year after the spring equinox on March 21. Determine L'(t), and use it to calcu 41. y = tan(0 + cos 0) 42. y = 2x2 late the rate that the length of the days are changing on March 25, April 30 and June 10. Discuss what the results say about the changing day length in 43. y = e2-912 44. y = cos'(e40) the spring in Moscow In Exercises 45-74, compute the derivative using derivative rules that have 83. The function L(1) = 12 + 3.4 sin( 35 () models the length of a day from sunrise to sunset in Sapporo, Japan, where / is the day in the year been introduced so far. after the spring equinox on March 21. Determine L'(r), and use it to cal- 45. y = tan(x2 + 4x) 46. y = sin(x2 + 4x) culate the rate that the length of the days are changing on December 1, january 1, and February 1. Discuss what the results say about the changing 47. y = x cos(1 - 3.x) 48. y = sin(x2) cos(x2) day length in the late fall and winter in Sapporo. 49. y' = (41 + 9)1/2 50. y = (z + 1)*(2z - 1)3 84. The general shape of the graph of S(1) = Are- for A, k > 0 is shown in Figure 2(A). There are two points on the graph where the tan- 51. y = (x + cosx)-4 52. = sin(cos(sin x)) gent line is horizontal and therefore where S'(1) = 0. Determine f in terms of k for these points by solving S'(1) = 0. 53. y = vsin x cos x 54. y = (9- (5 -2x4)?)3 55. y = (cos 6x + sin .x2) 1/2 56. y = (x + 1) 1/2 x + 2 57. y = tan' x + tan(x3) 58. y = V4 - 3 cos.x 59. y = ( 2+ 1 60. y = (cos' x + 3 cos x + 7)9 (A) (B) 61. y= cos(1 + x) 62. y = sec( 12 - 9) FIGURE 2 1 + cos .x 63. y = cot (x5) 64. y = - cos(1/x) 85. The general shape of the graph of S(1) = Ate-" for A, k > 0 is 1+ .x2 shown in Figure 2(B). There are two points on the graph where the tan- gent line is horizontal and therefore where S'(t) = 0. Determine / in terms 65. y = (1 + cor(x4 + 1)) 66. y = 4e-* + 7e-2x of k for these points by solving S'(t) = 0