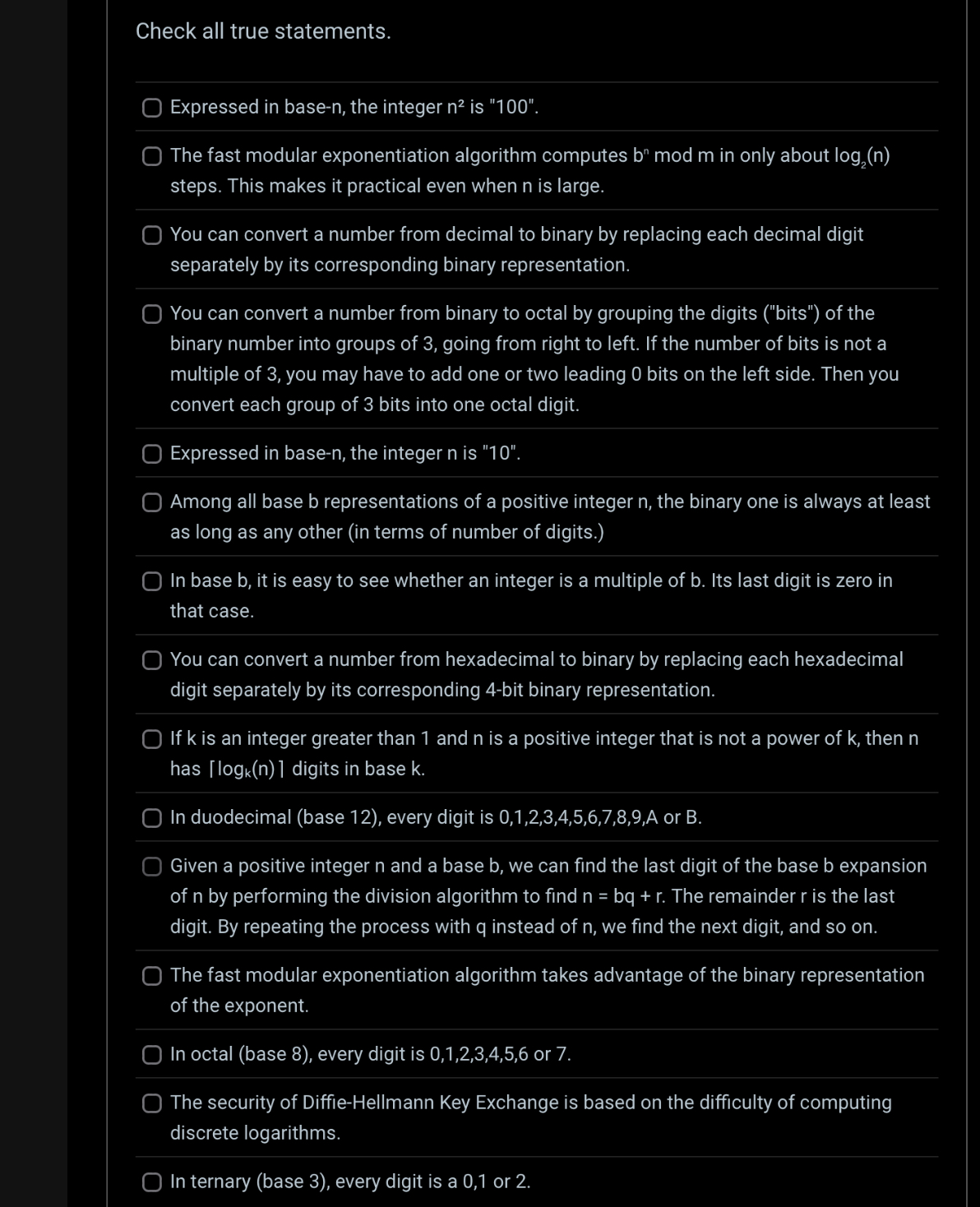
Check all true statements.Expressed in base$-$n$,$ the integer $\backslash (\backslash$mathrm$\{$n$\}^\{2\}\backslash )$ is $"100".$The fast modular exponentiation algorithm computes bn mod $\backslash ($ m $\backslash )$ in only about $\backslash (\backslash$log $\_\{2\}(\backslash$mathrm$\{$n$\})\backslash )$ steps. This makes it practical even when n is large.You can convert a number from decimal to binary by replacing each decimal digit separately by its corresponding binary representation.You can convert a number from binary to octal by grouping the digits $("$bits$")$ of the binary number into groups of $3,$ going from right to left. If the number of bits is not a multiple of $3,$ you may have to add one or two leading $0$ bits on the left side. Then you convert each group of $3$ bits into one octal digit.Expressed in base$-$n$,$ the integer n is $"10".$Among all base b representations of a positive integer n $,$ the binary one is always at least as long as any other $($in terms of number of digits.$)$In base b$,$ it is easy to see whether an integer is a multiple of b$.$ Its last digit is zero in that case.You can convert a number from hexadecimal to binary by replacing each hexadecimal digit separately by its corresponding $4-$bit binary representation.If $\backslash ($ k $\backslash )$ is an integer greater than $1$ and n is a positive integer that is not a power of k $,$ then n has $\backslash (\backslash$left$[\backslash$log $\_\{$k$\}($n$)\backslash$right$\backslash$rceil $\backslash )$ digits in base $\backslash ($ k $\backslash ).$In duodecimal $($base $12),$ every digit is $\backslash (0,1,2,3,4,5,6,7,8,9,\backslash$mathrm$\{$~A$\}\backslash )$ or B $.$Given a positive integer $\backslash ($ n $\backslash )$ and a base $\backslash ($ b $\backslash ),$ we can find the last digit of the base $\backslash ($ b $\backslash )$ expansion of $\backslash ($ n $\backslash )$ by performing the division algorithm to find $\backslash (\backslash$mathrm$\{$n$\}=\backslash$mathrm$\{$bq$\}+\backslash$mathrm$\{$r$\}\backslash ).$ The remainder r is the last digit. By repeating the process with $\backslash ($ q $\backslash )$ instead of $\backslash ($ n $\backslash ),$ we find the next digit, and so on$.$The fast modular exponentiation algorithm takes advantage of the binary representation of the exponent.In octal $($base $8),$ every digit is $\backslash (0,1,2,3,4,5,6\backslash )$ or $7.$The security of Diffie$-$Hellmann Key Exchange is based on the difficulty of computing discrete logarithms.In ternary $($base $3),$ every digit is a $0,1$ or $2.$