check on ur computer

please check on your computer it is so clean

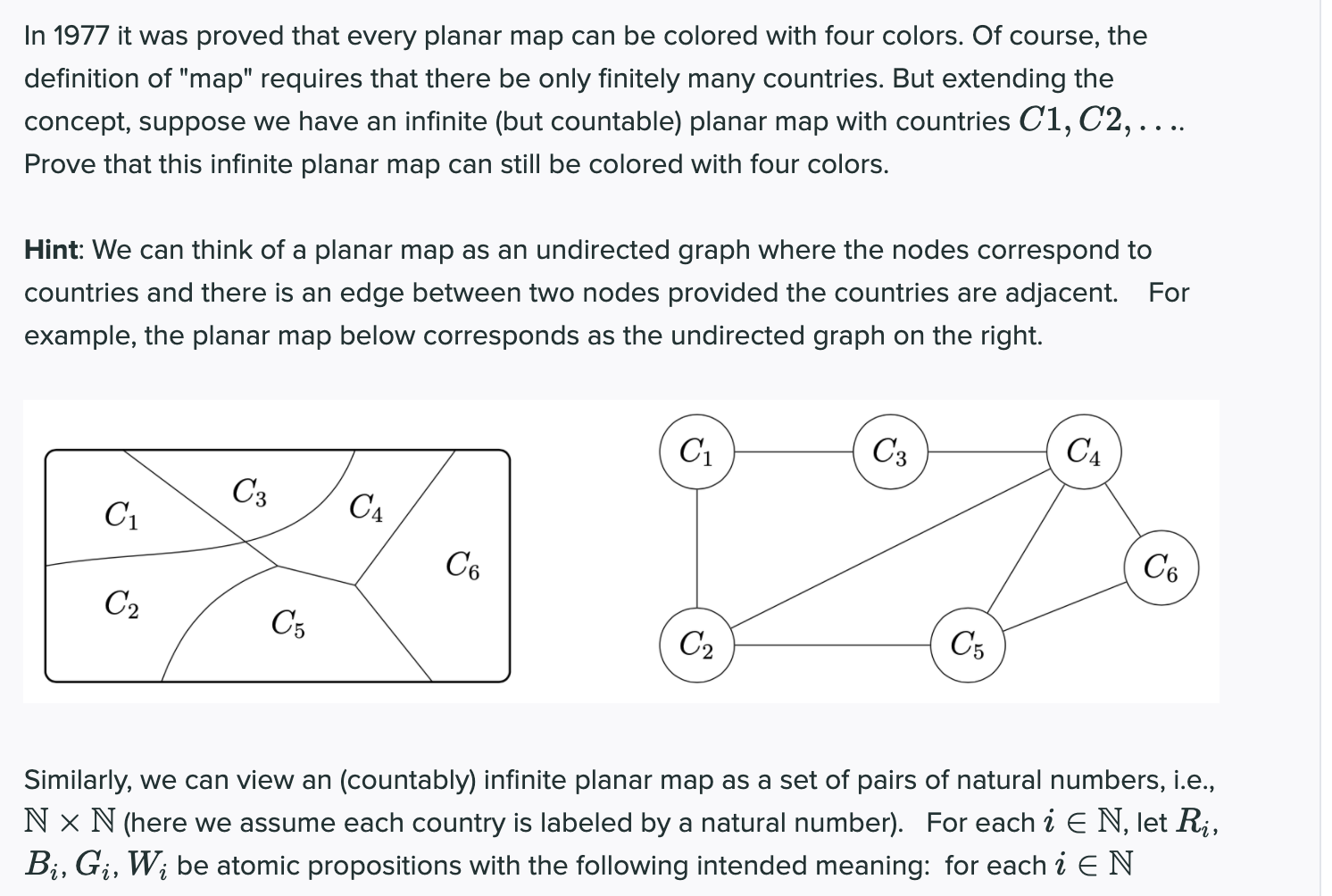
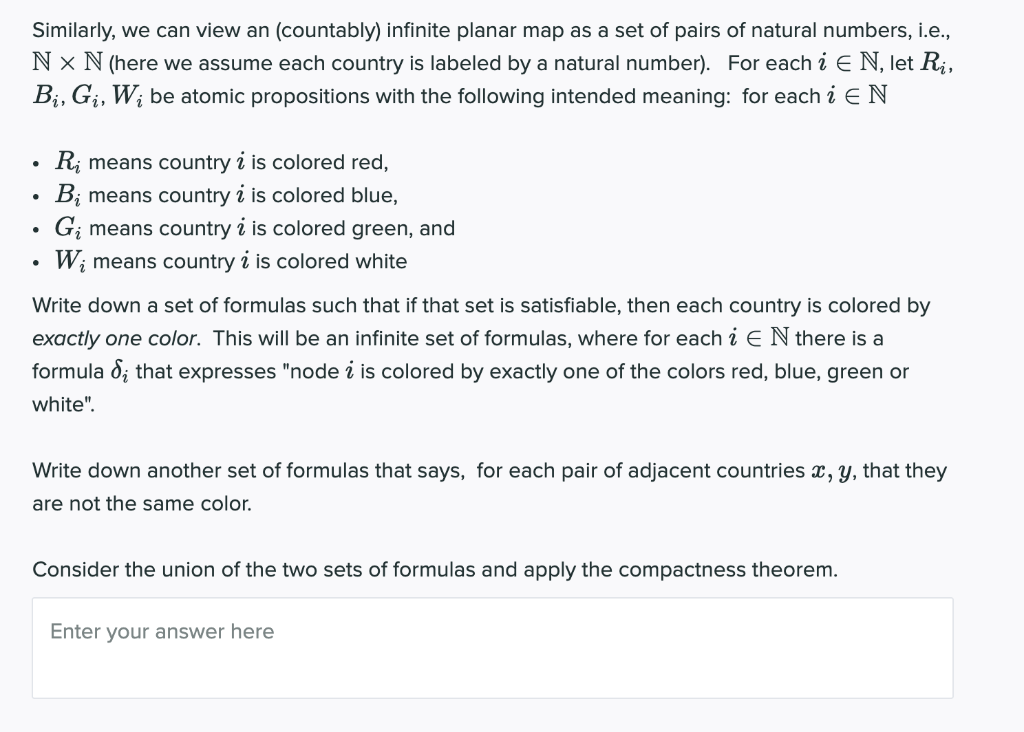
In 1977 it was proved that every planar map can be colored with four colors. Of course, the definition of "map" requires that there be only finitely many countries. But extending the concept, suppose we have an infinite (but countable) planar map with countries C1, C2, .... Prove that this infinite planar map can still be colored with four colors. Hint: We can think of a planar map as an undirected graph where the nodes correspond to countries and there is an edge between two nodes provided the countries are adjacent. For example, the planar map below corresponds as the undirected graph on the right. C1 C3 C4 C3 C1 C4 C6 Co C2 C5 C2 C5 Similarly, we can view an (countably) infinite planar map as a set of pairs of natural numbers, i.e., Nx N (here we assume each country is labeled by a natural number). For each i E N, let Ri, Bi, Gi, Wibe atomic propositions with the following intended meaning: for each i EN Similarly, we can view an (countably) infinite planar map as a set of pairs of natural numbers, i.e., Nx N (here we assume each country is labeled by a natural number). For each i E N, let Ri, Bi, G, W; be atomic propositions with the following intended meaning: for each i EN . 1 . R; means country i is colored red, B; means country i is colored blue, G means country i is colored green, and W; means country i is colored white Write down a set of formulas such that if that set is satisfiable, then each country is colored by exactly one color. This will be an infinite set of formulas, where for each i E N there is a formula di that expresses "node i is colored by exactly one of the colors red, blue, green or white". Write down another set of formulas that says, for each pair of adjacent countries x, y, that they are not the same color. Consider the union of the two sets of formulas and apply the compactness theorem. Enter your answer here In 1977 it was proved that every planar map can be colored with four colors. Of course, the definition of "map" requires that there be only finitely many countries. But extending the concept, suppose we have an infinite (but countable) planar map with countries C1, C2, .... Prove that this infinite planar map can still be colored with four colors. Hint: We can think of a planar map as an undirected graph where the nodes correspond to countries and there is an edge between two nodes provided the countries are adjacent. For example, the planar map below corresponds as the undirected graph on the right. C1 C3 C4 C3 C1 C4 C6 Co C2 C5 C2 C5 Similarly, we can view an (countably) infinite planar map as a set of pairs of natural numbers, i.e., Nx N (here we assume each country is labeled by a natural number). For each i E N, let Ri, Bi, Gi, Wibe atomic propositions with the following intended meaning: for each i EN Similarly, we can view an (countably) infinite planar map as a set of pairs of natural numbers, i.e., Nx N (here we assume each country is labeled by a natural number). For each i E N, let Ri, Bi, G, W; be atomic propositions with the following intended meaning: for each i EN . 1 . R; means country i is colored red, B; means country i is colored blue, G means country i is colored green, and W; means country i is colored white Write down a set of formulas such that if that set is satisfiable, then each country is colored by exactly one color. This will be an infinite set of formulas, where for each i E N there is a formula di that expresses "node i is colored by exactly one of the colors red, blue, green or white". Write down another set of formulas that says, for each pair of adjacent countries x, y, that they are not the same color. Consider the union of the two sets of formulas and apply the compactness theorem. Enter your answer here