class BinarySearchTree: def __init__(self): # your code here def add(self, value): # your code here def find(self, value): # your code here def __str__(self): # your code here

"""DO NOT MODIFY ANYTHING BELOW THIS LINE""" def test01(): narglist = [1] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree)

def test02(): narglist = [1, 2, 3] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree)

def test03(): narglist = [2, 1, 3] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree)

def test04(): narglist = [5, 3, 1, 2] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree)

def test05(): narglist = [4, 3, 2, 1, 5, 6] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree)

def test06(): narglist = [4, 3, 1, 2, 6, 5] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree)

def test07(): narglist = [1, 2, 3] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree.find(3))

def test08(): narglist = [2, 1, 3] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree.find(3))

def test09(): narglist = [5, 3, 1, 2] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree.find(3))

def test10(): narglist = [4, 3, 2, 1, 5, 6] tree = BinarySearchTree() for narg in narglist: tree.add(narg) return str(tree.find(3))

def trees_01(test_num): test_func = globals()['test{0}'.format(test_num)] return test_func()

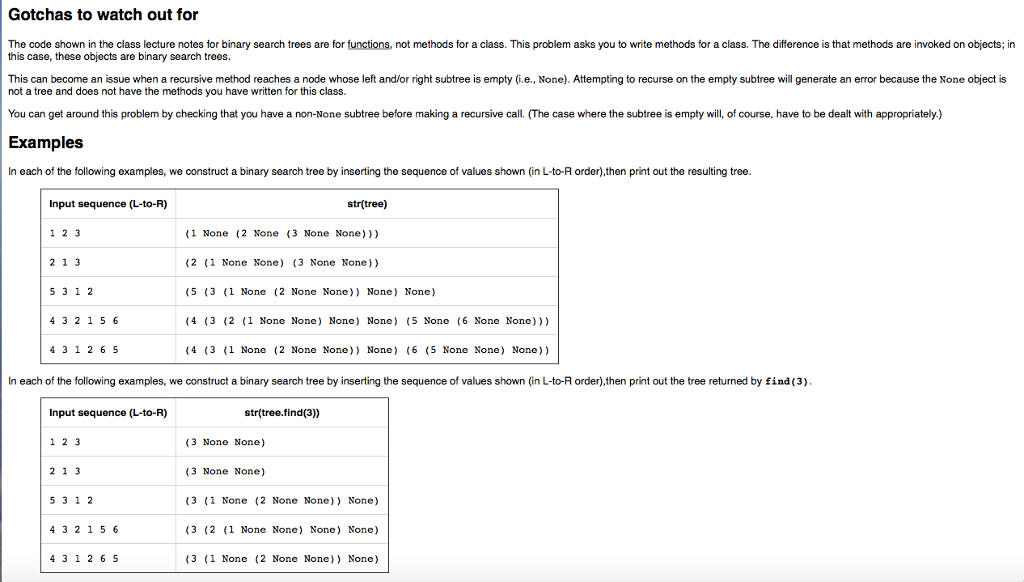
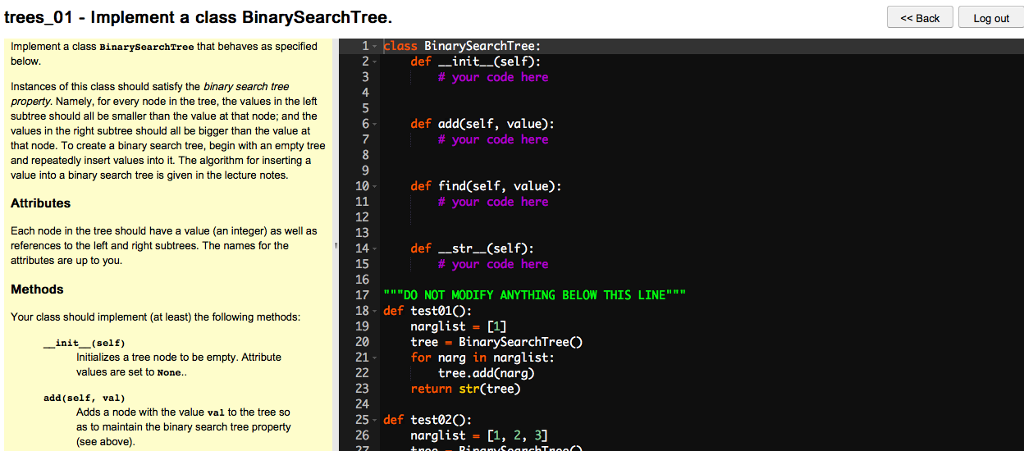
CSc 120: Binary Search Trees Expected Behavior Implement a class BinarysearchTree that behaves as specified below Instances of this class should satisfy the binary search tree property. Namely, for every node in the tree, the values in the left subtree should all be smaller than the value at that node; and the values in the right subtree should all be bigger than the value at that node. To create a binary search tree, begin with an empty tree and repeatedly insert values into it. The algorithm for inserting a value into a binary search tree is given in the lecture notes. Attributes Each node in the tree should have a value (an integer) as well as references to the left and right subtrees. The names for the attributes are up to you Methods Your class should implement (at least) the following methods: -init?(self) add (self, val) find(self, val) Initializes a tree node to be empty. Attribute values are set to Nono Adds a node with the value val to the tree so as to maintain the binary search tree property (see above) Returns: a reference to the tree node with value val if it exists, None otherwise. str-(self) Returns a strngrepresentation of the tree. For the purposes of this assignment, this is defined as follows. Given a tree T lf T ?S None ie empty return the string None the quotation marks s Otherwise, suppose that T has a root node with value val and left and right subtrees Tieft and Tright Return the string ply indicate that the value s a string they are not part of the s n g t e f (Kid )kormat( val, str(Tiofe), strTigh CSc 120: Binary Search Trees Expected Behavior Implement a class BinarysearchTree that behaves as specified below Instances of this class should satisfy the binary search tree property. Namely, for every node in the tree, the values in the left subtree should all be smaller than the value at that node; and the values in the right subtree should all be bigger than the value at that node. To create a binary search tree, begin with an empty tree and repeatedly insert values into it. The algorithm for inserting a value into a binary search tree is given in the lecture notes. Attributes Each node in the tree should have a value (an integer) as well as references to the left and right subtrees. The names for the attributes are up to you Methods Your class should implement (at least) the following methods: -init?(self) add (self, val) find(self, val) Initializes a tree node to be empty. Attribute values are set to Nono Adds a node with the value val to the tree so as to maintain the binary search tree property (see above) Returns: a reference to the tree node with value val if it exists, None otherwise. str-(self) Returns a strngrepresentation of the tree. For the purposes of this assignment, this is defined as follows. Given a tree T lf T ?S None ie empty return the string None the quotation marks s Otherwise, suppose that T has a root node with value val and left and right subtrees Tieft and Tright Return the string ply indicate that the value s a string they are not part of the s n g t e f (Kid )kormat( val, str(Tiofe), strTigh