Class FlightPath

You are going to define the class FlightPath to model a flight path as a sequence of straight-line segments in 2D space. Each segment is defined by three fields: a bearing, a distance (both doubles), and an id number (type int). The bearing is an angle in degrees, where zero degrees corresponds to north, 90 degrees to east, 180 degrees to south, etc. The distance is the length of the segment. Each segment can be identified by an id number. Notice how id numbers are handled as you continue to read the specification.

Your class needs to implement only the methods listed below. Your implementation of the class FlightPath must make use of a linked list to represent the flight path. For example, this flight path:

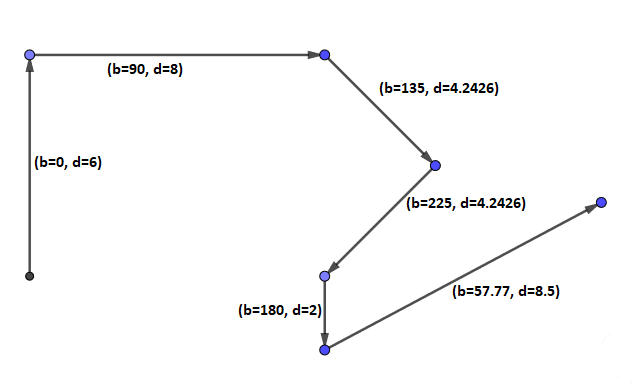
could be represented by this linked list:

Here is are key class invariants your class must guarantee:

Every bearing is a positive number in the following range: 0

Every distance is a positive number: 0

No segment shall have a distance of zero. If the distance works out to zero (as the result of compressing the flight path, for example), eliminate the segment.

Duplicate id numbers are not allowed.

Segments are always maintained in the liked list in order by id number, lowest to highest.

Here is the class specification. I have not specified what the preconditions are and what the methods should do if preconditions are not met. I leave that to you to determine based on discussions we've had in class.

Methods	Descriptions
FlightPath(String s)	Construct a FlightPath based on a string which contains a series of numbers separated by whitespace. The numbers are always in pairs: a bearing followed by a distance. For example, this statement should create the flight path illustrated in the example above: FlightPath fp = new FlightPath( "0 6 90 8 135 4.24264 225 4.24264 180 2 61.93 8.5" ); Notice that the parameter does not specify id numbers. Instead, the constructor initializes these. Segments are added to the flight path in the order specified by the parameter string, and id numbers are added beginning with 10 for the first segment, 20 for the second, etc. This would also be a legal statement: FlightPath fp = new FlightPath( "45 5.6 225 5.6 88.5 6.8" );
FlightPath(FlightPath fp)	Construct a FlightPath that is a duplicate (a deep copy) of the one provided without modifying fp.
int segments( )	Returns the number of segments in this FlightPath.
void addSegment(int id, double bearing, double distance)	Add a new segment to this FlightPath. The location of the segment in the linked list is determined by the id number. If a segment with the same id number already exists in the list, the new data replaces the old data in that segment and the number of segments in the flight path does not change.
double deleteSegment(int id)	If a segment with the specified id exists in this FlightPath, delete that segment and return its distance; otherwise return 0.0.
double getBearing(int id)	Return the bearing for the specified segment; return -1 if no such segment exists.
double tripLength( )	Return the total length of the trip defined by this FlightPath. The trip length is the total length of all the segments.
double directDistance( )	Return the distance of a direct, single-straight-line path from the starting point to the finish for this FlightPath. This requires a bit of trig. Draw a sketch to help you visualize it. TIP: Consider the N-S and E-W components of the overall distance separately, and then combine them to get the answer.
void compress( )	See instructions below for this mutator method.
boolean equals(Object o)	Override the equals method in an appropriate way. Two FlightPath objects are considered to be equal if they describe the same flight path. The id numbers are not relevant -- they should not be considered in the test for equality.
String toString( )	See instructions below for the string formatting requirements.
String description( )	See instructions below for the string formatting requirements.
static FlightPath reversePath(FlightPath a)	Returns a new FlightPath that describes a path that is the exact reverse of the one defined by the parameter without changing the FlightPath object referenced by the parameter. For example, the reverse of the flight path illustrated above would have this toString representation: "[(b=241.93, d=8.5), (b=0.0, d=2.0), (b=45.0, d=4.2426), (b=315.0, d=4.2426), (b=270.0, d=8.0), (b=180.0, d=6.0)]" The segment id numbers in the new FlightPath should be 10, 20, ... regardless of what the id numbers are in the parameter FlightPath. Notice this is a static method. How will this impact your implementation? IMPORTANT: A key requirement for this method is that it must make use of a private, recursive methodto create any FlightPath that has one or more segments.

IMPORTANT: Be aware that special care is required to ensure that all class invariants are satisfied for every FlightPath object.

The 'compress' Method

The 'compress' method is a mutator method that "compresses" this FlightPathobject by combining each pair of segments into a single segment that traverses the same space. For example, if the flight path described by the illustration above were compressed, after the operation was complete, it would have this toString representation: "[(b=53.1301, d=10), (b=180.0, d=6.0), (b=75.0686, d=7.7621)]".

Here is an illustration of the compressed flight path:

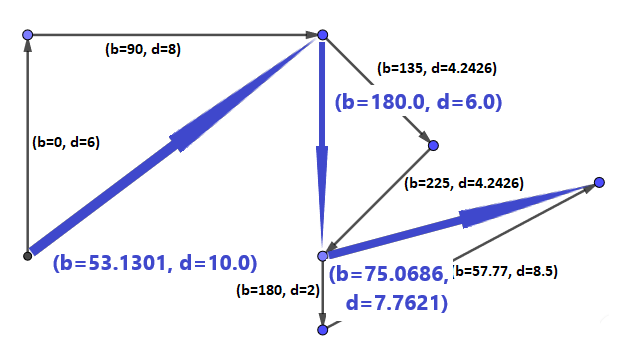
Four other details:

1. If the number of of segments was originally odd, then the final segment in the original path should remain as the final segment in the path after it has been compressed. 2. The segment id number for each "compressed" segment should be the same as the id number for the first of the two segments that were combined. In the example above, the segment id numbers would be 10, 30 and 50. 3. Remember that no segment may have a distance of 0. 4. [Added 11/10 after our discussion in class on 10/9.] The objective is to modify the existing linked list to change data in some existing segments and to remove some existing segments. You should not create any new Segment objects.

The 'toString' Method

The 'toString' method should produce output that represents the FlightPath in the following form:

The entire flight path is surrounded by square brackets: [ ].

Each segment shows the bearing and the distance in the following form: (b=1.2, d=3.45).

The bearing and distance are shown as floating point numbers, but the number of digits after the decimal point is rounded to the nearest 4. So, a segment with a bearing of 22.5 degrees and a distance of 3.456789 would be represented as: (b=22.5, d=3.4568). Notice that 4 digits are not always shown after the decimal point, but no more than 4 digits are shown after the decimal point.

Segment id values are not shown.

Multiple segments are separated by a comma and a single space.

Here are a few examples (quote marks are not part of the string -- they just mark the beginning and end of its contents):

The flight path shown in the diagram near the beginning of this document would be represented as follows: "[(b=0.0, d=6.0), (b=90.0, d=8.0), (b=135.0, d=4.2426), (b=225.0, d=4.2426), (b=180.0, d=2.0), (b=61.93, d=8.5)]"

( new FlightPath( "90 2 22.5 8.6" ) ).toString( ) ==> "[(b=90.0, d=2.0), (b=22.5, d=8.6)]"

( new FlightPath( "55.4 3" ) ).toString( ) ==> "[(b=55.4, d=3.0)]"

( new FlightPath( "" ) ).toString( ) ==> "[]"

The 'description' Method

The 'description' method should produce output that represents the FlightPath in a different way -- with each segment described in a separate line. Here are a few examples to illustrate the intended format (notice the presence of the "newline" character ' '):

( new FlightPath( "90 2 22.5 8.6" ) ).description( ) ==> "segment 10, bearing 90.0 degrees, distance 2.0 segment 20, bearing 22.5 degrees, distance 8.6"

( new FlightPath( "55.4 3" ) ).description( ) ==> "segment 10, bearing 55.4, distance 3.0"

( new FlightPath( "" ) ).description( ) ==> "no path"

IMPORTANT: A key requirement for this method is that it must make use of a private, recursive method to create the result for any FlightPath that has one or more segments.

Could you help me I'm really confuse about the compress methods and reversePath methods( shoulds have public and private methods for the reversePath).

Thank you

(b-90, d-8) (b-135, d-4.2426) (b-o, d-6) (b-225, d-4.2426) (b=57.77, d=8.5) (b:180, d=2)