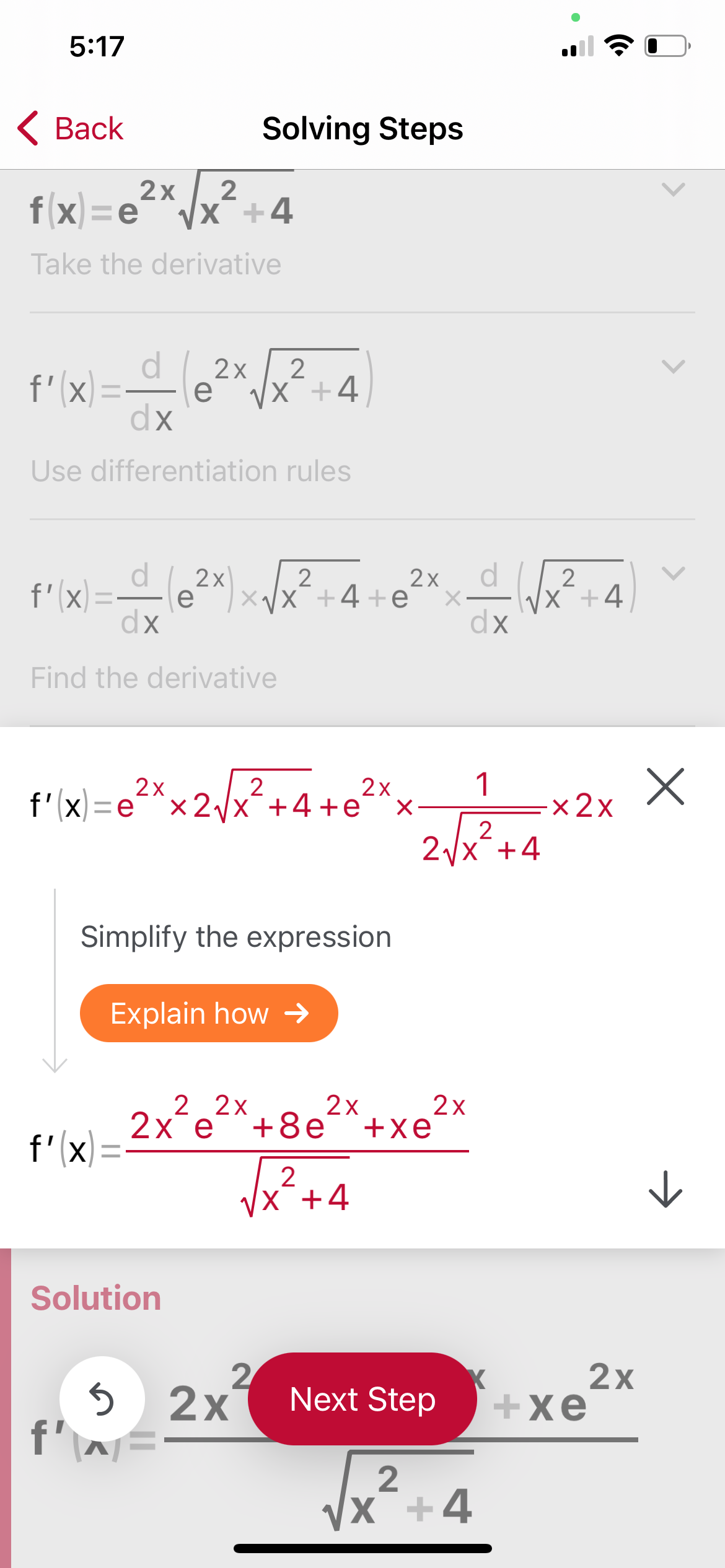
Question: code class = asciimath > f ( x ) = e ^ ( 2 x ) sqrt ( x ^ ( 2 ) +
code class"asciimath"fxexsqrtx Take the derivative fxddxexsqrtx Use differentiation rules fxddxextimes sqrtxextimes ddxsqrtx Find the derivative fxextimes sqrtxextimes sqrtxtimes x Simplify the expression fxxexexxexsqrtx Solution fOmega x Next Step xxex
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


