Coding exercise in MATLAB

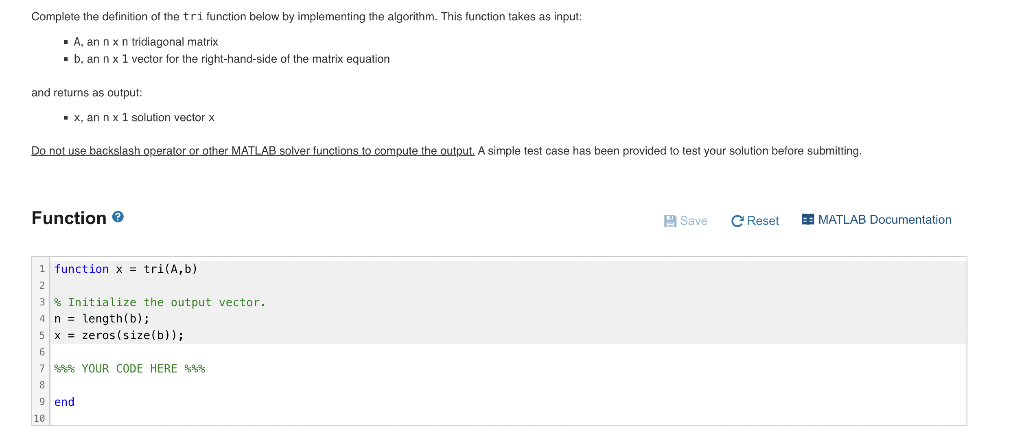
Solving tridiagonal systems of equations Consider the matrix problem Ax=b, where A is a tridiagonal matrix and b is a column vector with the form: A=d1a1000c1d2a2000c2d300000dn1an1000cn1dn,b=b1b2b3bn1bn diagonal. You may assume that pivoting is not necessary to solve the system. For more details, see page 180 of the textbook. input n,(ai),(bi),(ci),(di) for i=2 to n do didi(ai1/di1)ci1bibi(ai1/di1)bi1enddoxnbn/dnfori=n1to1step1doxi(bicixi+1)/di end do output (xi) Complete the definition of the tri function below by implementing the algorithm. This function takes as input: - A, an nn tridiagonal matrix - b, an n1 vector for the right-hand-side of the matrix equation and returns as output: - x, an n1 solution vector x Do not use backslash operator or other MATLAB solver functions to compute the output. A simple test case has been provided to test your solution before submitting. Function 3 Code to call your function