colours so that for every pair $\backslash ($ u$,$ v $\backslash )$ of adjacent vertices, $\backslash ($ u $\backslash )$ and $\backslash ($ v $\backslash )$ are assigned different colours.

The $\backslash (\backslash$quad $\backslash )$ of a graph $\backslash ($ G $\backslash ),$ denoted by $\backslash (\backslash$chi$($G$)\backslash ),$ is the smallest integer $\backslash ($ k $\backslash )$ for which graph $\backslash ($ G $\backslash )$ is $\backslash ($ k $\backslash )-$colorable. To show that $\backslash (\backslash$chi$($G$)=$k $\backslash ),$ you must show that the graph is $\backslash ($ k $\backslash )-$colourable and that the graph is not $\backslash (($k$-1)\backslash )-$colourable.

Q$4\mathrm{.}1$

$5$ Points

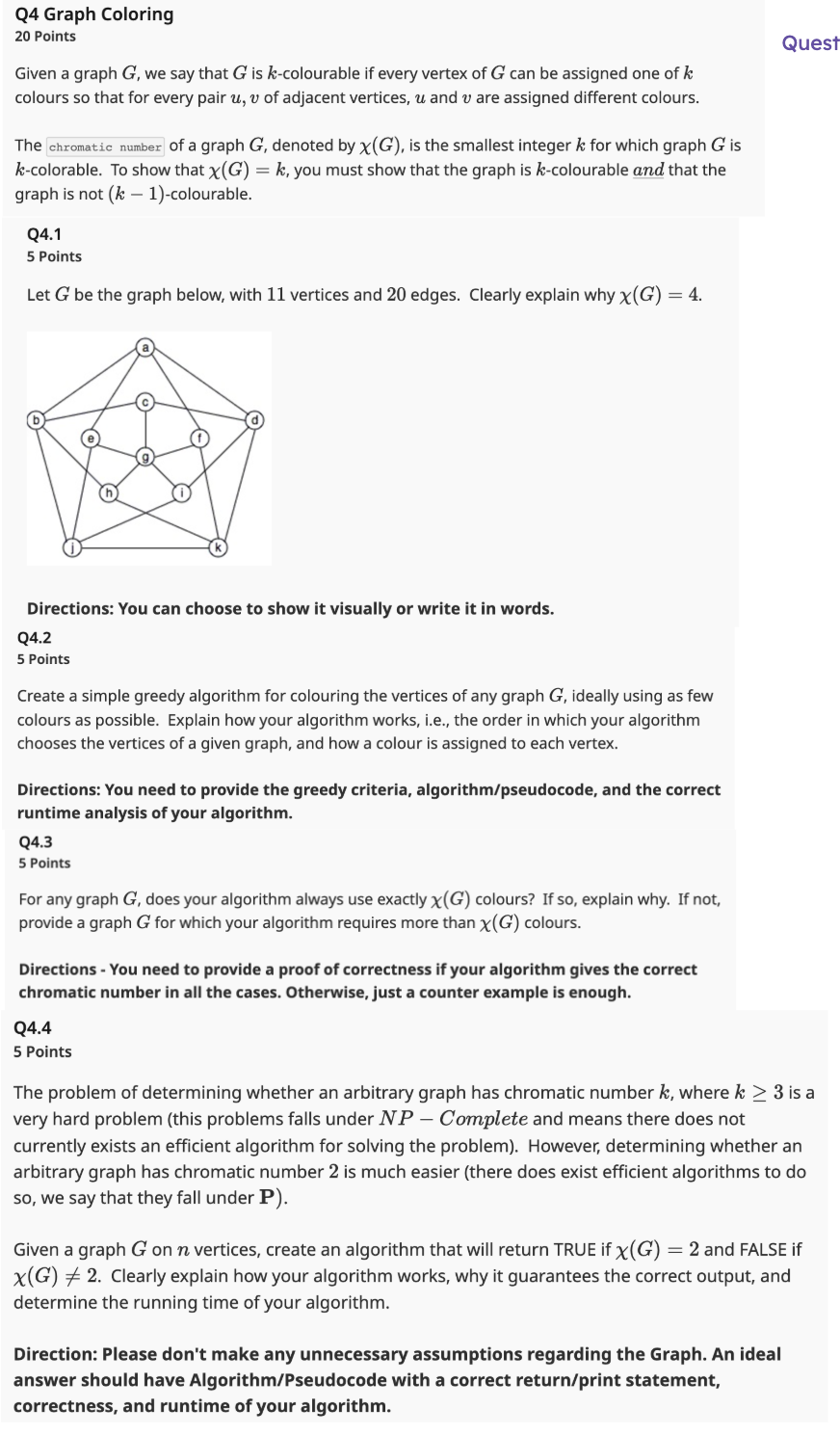
Let $\backslash ($ G $\backslash )$ be the graph below, with $11$ vertices and $20$ edges. Clearly explain why $\backslash (\backslash$chi$($G$)=4\backslash ).$

Directions: You can choose to show it visually or write it in words.

Q$4\mathrm{.}2$

$5$ Points

Create a simple greedy algorithm for colouring the vertices of any graph $\backslash ($ G $\backslash ),$ ideally using as few colours as possible. Explain how your algorithm works, i$.$e$.,$ the order in which your algorithm chooses the vertices of a given graph, and how a colour is assigned to each vertex.

Directions: You need to provide the greedy criteria, algorithm$/$pseudocode$,$ and the correct runtime analysis of your algorithm.

Q$4\mathrm{.}3$

$5$ Points

For any graph $\backslash ($ G $\backslash ),$ does your algorithm always use exactly $\backslash (\backslash$chi$($G$)\backslash )$ colours? If so$,$ explain why. If not, provide a graph $\backslash ($ G $\backslash )$ for which your algorithm requires more than $\backslash (\backslash$chi$($G$)\backslash )$ colours.

Directions $-$ You need to provide a proof of correctness if your algorithm gives the correct chromatic number in all the cases. Otherwise, just a counter example is enough.

Q$4\mathrm{.}4$

$5$ Points

The problem of determining whether an arbitrary graph has chromatic number $\backslash ($ k $\backslash ),$ where $\backslash ($ k $\backslash$geq $3\backslash )$ is a very hard problem $($this problems falls under $\backslash ($ N P$-\backslash )$ Complete and means there does not currently exists an efficient algorithm for solving the problem$).$ However, determining whether an arbitrary graph has chromatic number $\backslash (\backslash$mathbf$\{2\}\backslash )$ is much easier $($there does exist efficient algorithms to do so$,$ we say that they fall under $\backslash (\backslash$mathbf$\{$P$\}\backslash )).$

Given a graph $\backslash ($ G $\backslash )$ on $\backslash ($ n $\backslash )$ vertices, create an algorithm that will return TRUE if $\backslash (\backslash$chi$($G$)=2\backslash )$ and FALSE if $\backslash (\backslash$chi$($G$)$

eq $2\backslash ).$ Clearly explain how your algorithm works, why it guarantees the correct output, and determine the running time of your algorithm.

Direction: Please don't make any unnecessary assumptions regarding the Graph. An ideal answer should have Algorithm$/$Pseudocode with a correct return$/$print statement, correctness, and runtime of your algorithm.