Question: Comicdur the system described by Obtain the transfer function matrix of the system.5) Compute At for A = To I -2 - 3 using the


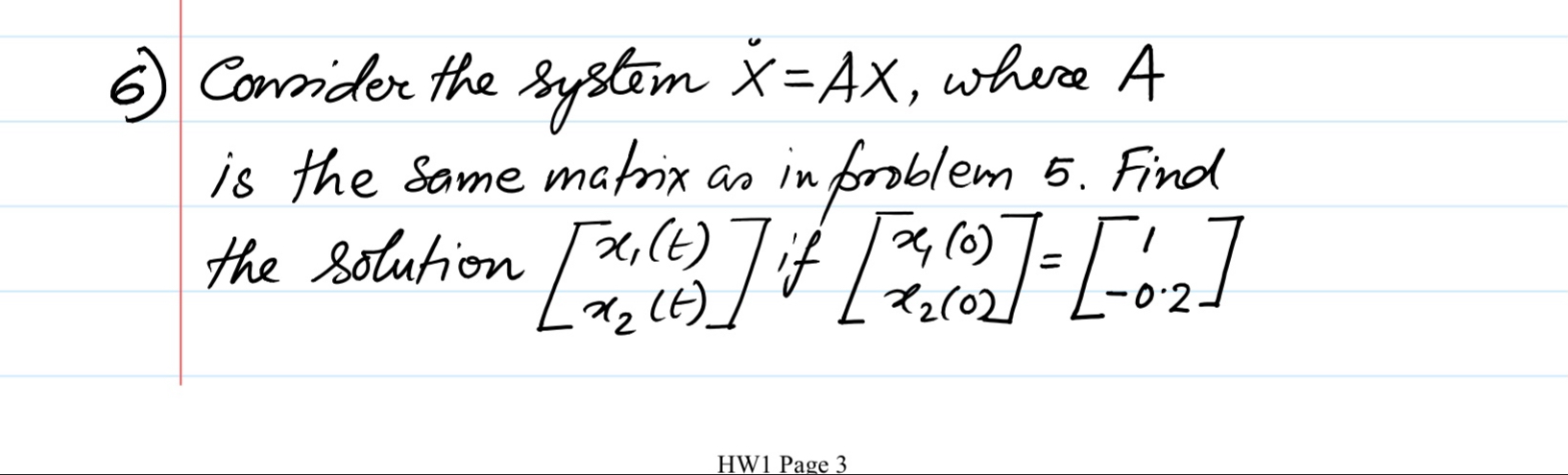
![At b eft = d [ ( SI- A )'] PAPE -1](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6703fcbe23a0d_5576703fcbe01202.jpg)
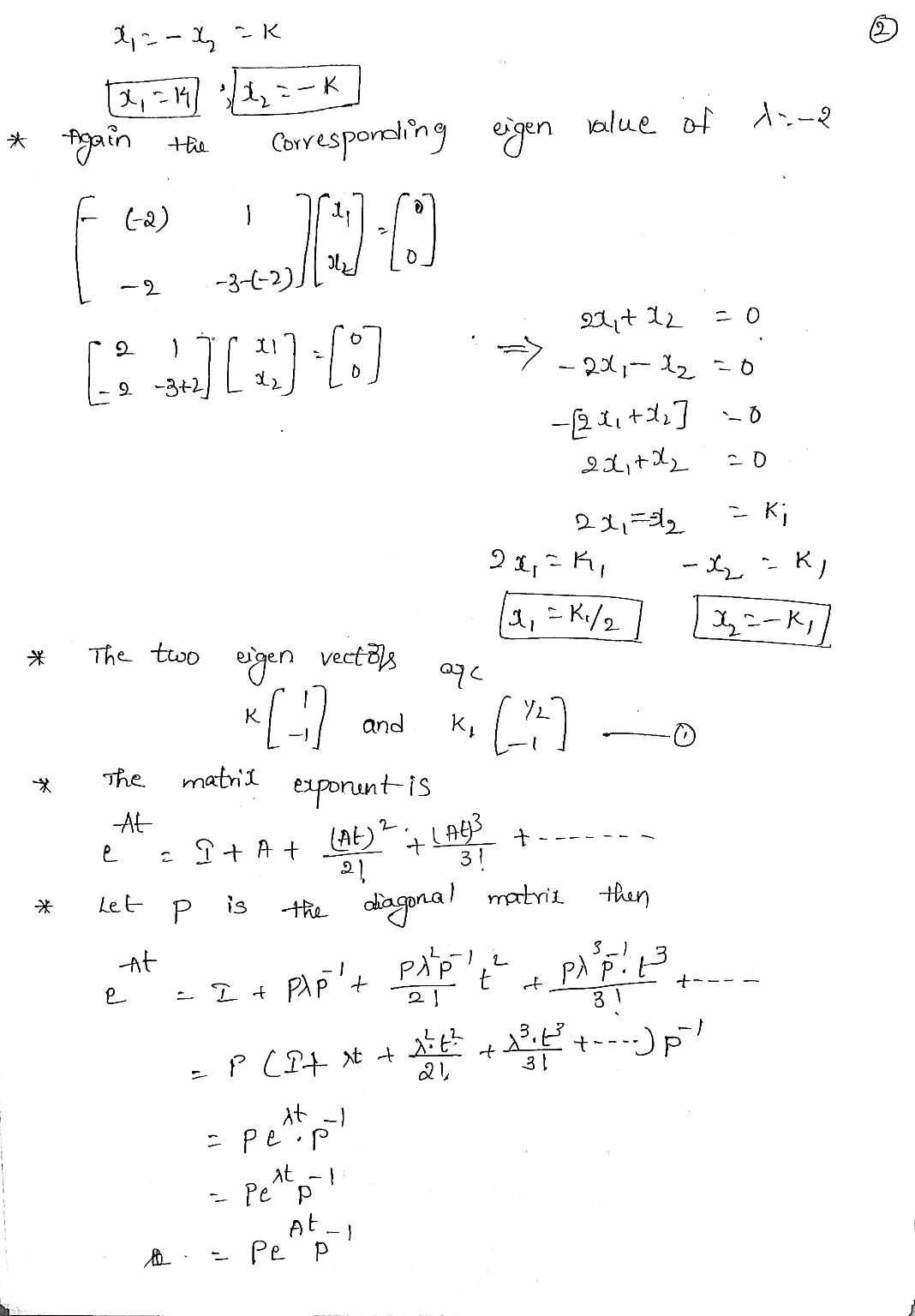
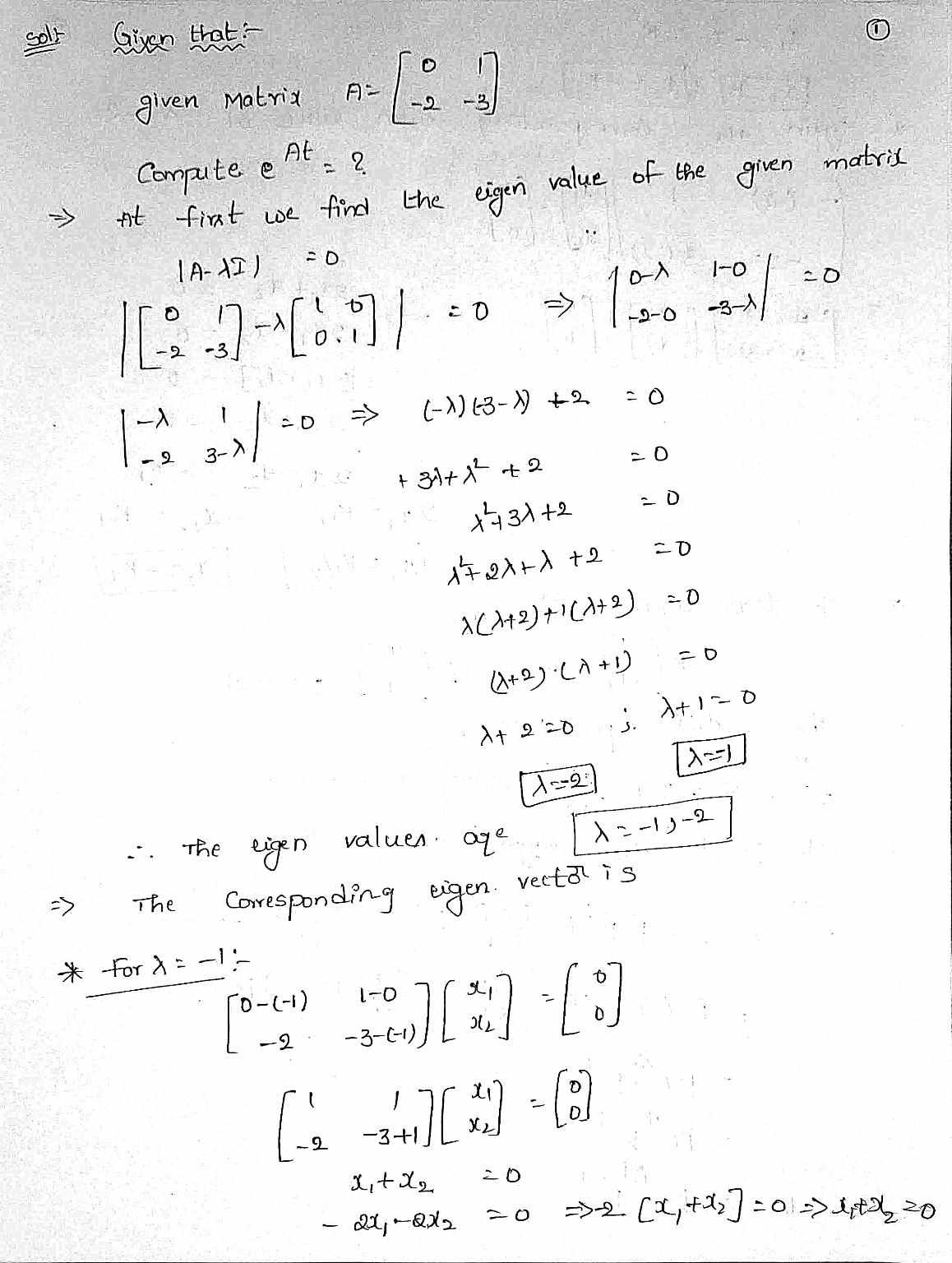



Comicdur the system described by Obtain the transfer function matrix of the system.5) Compute At for A = To I -2 - 3 using the following three methods: - a Direct series expansion of e At b eft = d [ ( SI- A )'] PAPE -1 At using the property e Pep ( Hint : for C use the diagonalizing P matrix6) Consider the system X= AX, where A is the Same matrix as in problem 5 . Find the Solution 2 2 (H) "Me, (6 ) 7if / 2, 10) 7 = [627 HW1 Page 3Page 4 7 ) for the A matrices in problems 5 & 3 , find the eigenvalues . Clearly show your work is determining the values .2 - -2 -K 2 2 - 19 1 2 - K * -Again Corresponding eigen value of 1s-2 (- 2 ) - 2 - 3- (-2 ) J L 204, + 12 = 0 - 201 1 - 12 = 0 - 0 2 2,t ( 2 = D - 9 - K J a , = Ki / 2 * The two eigen vectors age 1 = - K J and K , ( ": ] * The matrix exporunt is -At e = It At ( At)2. LAGS 2 1 31 * Let p is the diagonal matric then -At 2 1 t + . 3 1 31 = pe . p At - Pe p 1 . = Pe PSoll Given that given Matrix A= - 2 - 3 Compute e F = 2 At first we find the eigen value of the given matrix 10-1 1-0 - 2-0 - 3-1/ - A 1- 2 3- > =0 => ( - > ) (3 - 1) + 2 = 0 + 31+ 12 + 2 = 0 143 1 + 2 17 2 1 + 1 + 2 1 ( ) +2 ) + 1 ( 1 + 2 ) = 0 ( + 2 ) .(A + 1 ) 1=2: The eigen values . age 1 2 -13- 2 = > The Corresponding eigen vectol is * for > = - 1:- 0 - ( - 1 ) 1 - 0 - 2 . -3-(-1 ), 20 - 21-212 20 =2 [ 26, 72 ) = 01-> 1,124 20\f* = AX = -2 - 3, Hm = - 234-3x2 724 + (0 + 3 ) 26 2 = 0 X(#) ; D= # and Day - x2 = 0.X (D+3] -Them-Sum. = ( 2 + D ( 1+ 3 ] | 24 = 0 2) ( D + 3 D + 2 / 29 = 0) 24 = get cent 3 4 30 + 2 =0 gives - 1,-2 at - 24 Also 39(0) 2 1 * 2 (0 ) = - 0:2 2 ) 1 = 4.#62 7-0.12 - 9-262 46 - 62 = 1-012 = 0.8 en= - 0:8/ and 4 = 1 - 62 = 1408 Heall my (+ ) = \\1 8/ e - 10- sle 2+ sky(t ) = - (1.8 ) et H1 6/e 24Hop ": set up the characteristics equation. det ( A - > I)= 0 step ?: Substitute the values at A FI det Step 3: Simplify - 2 - 3 - X Step 4: calculate the determinant (- x)(-3 - 1) - (11 1-9)=0 itep s: simplify and use quadratic equation Lovenodq ( x + 1 ) ( x 12 ) =0 step G: silve for the exgenvalves. 1, = -1 , d2 : -2
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


