complete the problem

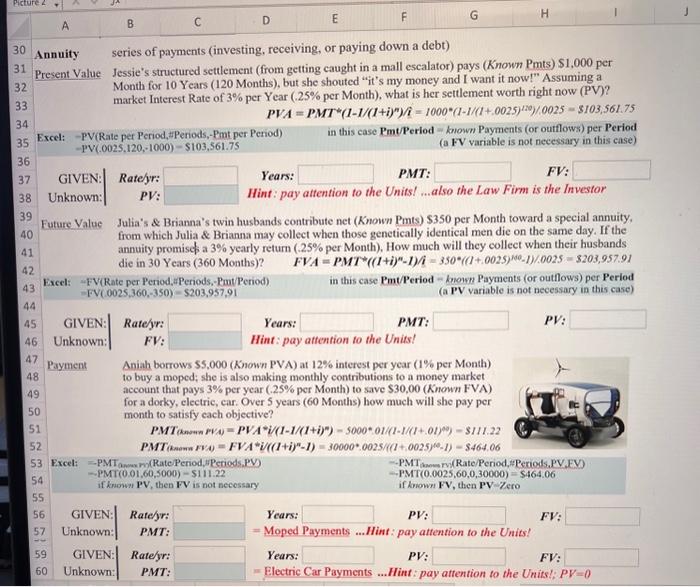
A B C D NOTE: Both Excel and Manual (calculator) processes are explained below, but we will use just processes (but feel free to try the other...). Please set up below by identifying the given variables and referencing those Cells (not the values) in your formulas John Mollica Time Value of Money Supplemental Legend: PV = Present Value FV - Future Value PVA - Present Value of an Annuity FVA - Future Value of an Annuity PMT - Paid at the Fnd of each Compounding Period (applies only to Annuity or Perpetuity; "due" if beginning) NOTES: - Exeel treats Investments as Outhows so in all excel functions (below), Payment(s) are preceded with a Negative Sign (-) - if Payments are Monthly, Interest is stated Yearly, and Periods are stated Yearly, then: Interest must first be Divided by 12 (to convert to Monthly) -and- MAKE SURE ALL Periods must be first be Multiplied by 12 (to convert to Monthly) UNITS MATCHI e.g. to determine Monthly Payments on a 30 Year mortgage at 6% per Year, Single Payment Present Value Nick wants to put aside enough of his lottery winnings to have $600,000 (Known FV) to put toward his triplet daughters' college education in 20 years. How much (PV) should he contribute toward a CD that pays 6% interest ber year PV=FV/(1+i)n600000/(1+.06)205187,082.84 Excel: = PV(Rate per Period, HPeriods Pmets per Reriod, FV) in this case there is only one (unknown, PV) Investment, so: PV(,06,20,0,600000)=$187,082,84 Pmt/Period - Zero, - and- FV = the kiown/desired FV after (n) Periods Future Value Loan shark, Taras lent $10,000 (Known PV) at 20% per month to developer. Alberto to bribe land appraiser, Julia so he may secure a loan from banker, Wilhelm. How much (FV) will Alberto owe Taras in 1 year ( 12 months)? FV=PV(1+i)n10000(1+2)nz=589,161 Fxeel: -FV(Rate per Period,aPeriods, Pmts per Period,-PV) FV(.2,12,0,10000)$89,161 in this case there is only one (known PV) Romt (or cutilow), so: 27 28 GIVEN: : Rate/mo: Years: PMT: PV: Unknown: FV: Hint: pay attention to the Units! ...also Taras is the Investor Annuity series of payments (investing, receiving, or paying down a debt) 30 Annuity series of payments (investing, receiving, or paying down a debt) 31 Present Value Jessie's structured settlement (from getting caught in a mall escalator) pays (Known Pmts) \$1,000 per 32 33 Month for 10 Years (120 Months), but she shouted "it's my money and I want it now!" Assuming a market Interest Rate of 3% per Year (.25% per Month), what is her settlement worth right now (PV)? PVA=PMT(11/(I+i)n)/I=1000(11/(I+.0025)120)/0025=$103,561.75 34 35 Excel: -PV(Rate per Period, Periods, Pent per Period) in this case Pmt/Period = known Payments (or outflows) per Period -PV(.0025,120,-1000) $103,561.75 (a FV variable is not necessary in this case) 36 37 GIVEN: Ratejr: Years: PMT: FV: 38 Unknown: PV : Hint : pay attention to the Units! also the Law Firm is the Investor 39 Future Value Julia's \& Brianna's twin husbands contribute net (Known Pmts) \$350 per Month toward a special annuity, from which Julia \& Brianna may collect when those genetically identical men die on the same day. If the annuity promiso a 3% yearly return (.25\% per Month), How much will they collect when their husbands 42 43 Excel: -FV(Rate per Period,uPeriods,-Pmt/Period) FV (0025,360,350)=$203,957,91 in this case PmU/Period - known Payments (or outhlows) per Period (a PV variable is not necessary in this case) 44 45 Years: PMT: PV: 46 Hint: pay attention to the Units! Aniah borrows 55,000 (Known PVA) at 12% interest per year (1\% per Month) to buy a moped; she is also making monthly contributions to a money market account that pays 3% per year (.25\% per Month) to save $30,00 (Known FVA) for a dorky, electric, car. Over 5 years ( 60 Months) how much will she pay per month to satisfy cach objective? PMT(2aumFVA=FVAi((I+i)n1)=300000025/(I+0025)101)5464.06 PMT(0.0025,60,0,30000)=$464.06 -PMT(0.01,60,5000) $111.22 if known FV, then PV-Zero Years: PV : FV Unknown: PMT: = Moped Payments ...Hint: pay attention to the Units! 59 GIVEN: Ratefyr: Years: PV: FV: Unknown: PMT : = Electric Car Payments .Hint: pay attention to the Units:; PV=0 Unknown: PV: Hint: pay attention to the Units! ...also the Law Firm is the Investor Future Value Julia's \& Brianna's twin husbands contribute net (Known Pmts) $350 per Month toward a special annuity, from which Julia \& Brianna may collect when those genetically identical men die on the same day. If the annuity promisco a a 3% yearly return (.25\% per Month). How much will they collect when their husbands die in 30 Years (360 Months)? ?VA =PMT((I+i)nI)/i350((t+.0025)1601)(0025=5203,957.91 Excel: =FV(Rate per Period,uPeriods,-Pmt/Period) in this case Pmt/Period = kmown Payments (or outflows) per Period FV (0025,360,350)$203,957,91 (a PV variable is not necessary in this case) GIVEN: Unknown: Ratefyr: FV: Years: PMT: Hint: pay attention to the Units! PV : PV: Payment Aniah borrows $5,000 (Known PVA) at 12% interest per year ( 1% per Month) to buy a moped; she is also making monthly contributions to a money market account that pays 3% per year (.25\% per Month) to save $30,00 (Known FVA) for a dorky, electric, car. Over 5 years ( 60 Months) how much will she pay per month to satisfy each objective? PMT(nawnPVA)=PVAi(11/(I+i)n)=5000.01/(I1/(I+.0I))=$111.22PMT(neenRVA=FVAi((I+i)n1)=30000.0025/(I+.0025)001)5464.06 -PMT (0.01.60.5000)$111.22 =PMT(0.0025,60,0,30000)$464.06 if knows? PV, then FV is not necessary if known FV, then PV Zero \begin{tabular}{r|r|r|r} GIVEN: & Rateyr: & Years: \\ Unknown: & PMT: & Moped Payments ...Hint: pay attention to the Units! \end{tabular} Intemal Rate of Return An intial investment of $250,000 returns the following at the end of years 1-5: (only Excel used) $50,000;$60,000;$80,000;$80,000; and $60,000 What is the Rate of Return on the investment