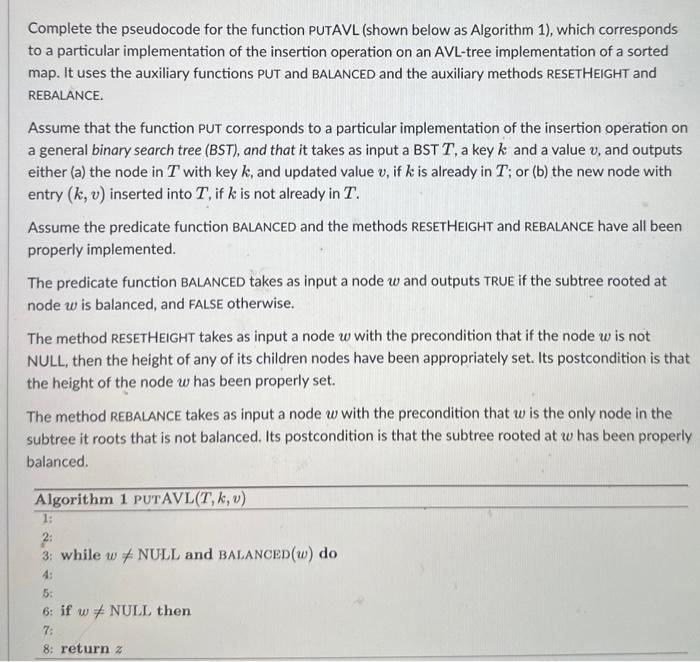
Complete the pseudocode for the function PUTAVL (shown below as Algorithm 1), which corresponds to a particular implementation of the insertion operation on an AVL-tree implementation of a sorted map. It uses the auxiliary functions PUT and BALANCED and the auxiliary methods RESETHEIGHT and REBALANCE. Assume that the function PUT corresponds to a particular implementation of the insertion operation on a general binary search tree (BST), and that it takes as input a BST T, a key k and a value v, and outputs either (a) the node in T with key k, and updated value v, if k is already in T; or (b) the new node with entry (k,v) inserted into T, if k is not already in T. Assume the predicate function BALANCED and the methods RESETHEIGHT and REBALANCE have all been properly implemented. The predicate function BALANCED takes as input a node w and outputs TRUE if the subtree rooted at node w is balanced, and FALSE otherwise. The method RESETHEIGHT takes as input a node w with the precondition that if the node w is not NULL, then the height of any of its children nodes have been appropriately set. Its postcondition is that the height of the node w has been properly set. The method REBALANCE takes as input a node w with the precondition that w is the only node in the subtree it roots that is not balanced. Its postcondition is that the subtree rooted at w has been properly balanced. Algorithm 1 PUTAVL (T,k,v) 1: 2: 3: while w= NULL and BALANCED (w) do 4: 5: 6: if w= NULL then 7: 8: return z Using Big-Oh notation, select tight characterizations of the worst-case running time and space complexity of the method PUTAVL, implemented in Algorithm 1 (as shown in the previous question), as a function of the number of entries n in the input AVL tree T. Assume that the predicate function BALANCED, and the methods RESETHEIGHT and REBALANCE, all run in constant time and use constant space in the worst-case. Also assume that PUT runs in time linear in the depth of the tree and uses a constant amount of space. - Time: - Space