Question: (computability and complexity): A vertex cover in an undirected graph G=(V,E) is a set of vertices U, so that every edge in E Whas at

(computability and complexity): A vertex cover in an undirected graph G=(V,E) is a set of vertices U, so that every edge in E Whas at least one end in U.

We'll define the following function:f(G,v)=minimal vertex cover that v belongs to

the input is an undirected graph G and a vertex v of G.

The function returns an natural number, that is the smallest size of vertex cover in G that v belongs to

1)Prove: If it is possible to compute f in a polynomial time then P=NP

2)Prove: If it is possible to calculate in a polynomial time function g(G,v), and it is guarenteed that 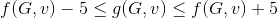(computability and complexity): A vertex cover in an undirected graph G=(V,E) is , then P=NP.

please explain every step you do so i can learn from your proof the best. thank you!

f(G,V) - 5

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

(computability and complexity): A vertex cover in an undirected graph G=(V,E) is a set of vertices U, so that every edge in E Whas at least one end in U. We'll define the following...

(computability and complexity): A vertex cover in an undirected graph G=(V,E) is a set of vertices U, so that every edge in E has at least one end in U. We'll define the following...

We have an undirected graph G =(V. E) with |V players, in which each player i controls exactly one, distinct vertex Vi e V. Each edge e E is associated with a nonnegative weight we. A cut is a...

(9 pts) Problem 20 in Chapter 4 (Greedy Algorithms). The input is a (undirected) graph where the nodes are towns and the edges represent the roads between them. Each edge is labeled with the maximum...

PROBLEM 2: VERTEX COVER Consider the following language from the text, VERTEXCOVER G, k) G is an undirected graph that has a k-node vertex cover] A k-node verter cover of a graph G- (V, E) is a set...

(a) A user complains that their web application Times Out after successfully connecting to a remote host, yet, an investigation with ping indicates the remote host is alive. Propose a cause of this...

There is an underlying undirected graph G = (V, E) with weights on the vertices, where the weight on vertex v is denoted by wv = d(v) (the degree of the vertex). Your goal is to find a vertex cover...

= Question 3: As input, we are given an undirected graph G (V, E) and a set of tokens T, where T| > |El. We have to assign a token t(e) e T to every edge e E E in such a way that: for every token t...

ertex Cover. Given an undirected graph G = ( V , E ) , a Vertex Cover is a set of vertices V V such that every edge e in E is incident on ( touches ) some vertex in V .

A path cover of a directed graph G = (V, E) is a set P of vertex-disjoint paths such that every vertex in V is included in exactly one path in P. Paths may start and end anywhere, and they may be of...

A 2-m-high sandy fill material was placed loosely at a relative density of 47%. Laboratory studies indicated that the maximum and minimum void ratios of the fill material are 0.92 and 0.53,...

True or False: If everyone had the same income, substandard housing would disappear.

systematic risk is measured by what? Standard Deviation Beta Alpha A Riskometer

5. Develop a scenario comparing two PH programs and involving the use of a CBA.

1. Have you selected an informative topic that will teach your audience members something new?

3 Are your motivations really ethical? Do you want to avoid talking about scholarship money because you think it will never materialize or because youre angry that the coach misled you?

3. Did you select an appropriate approach for your informative speech? Will your audience be able to clearly identify your approach?