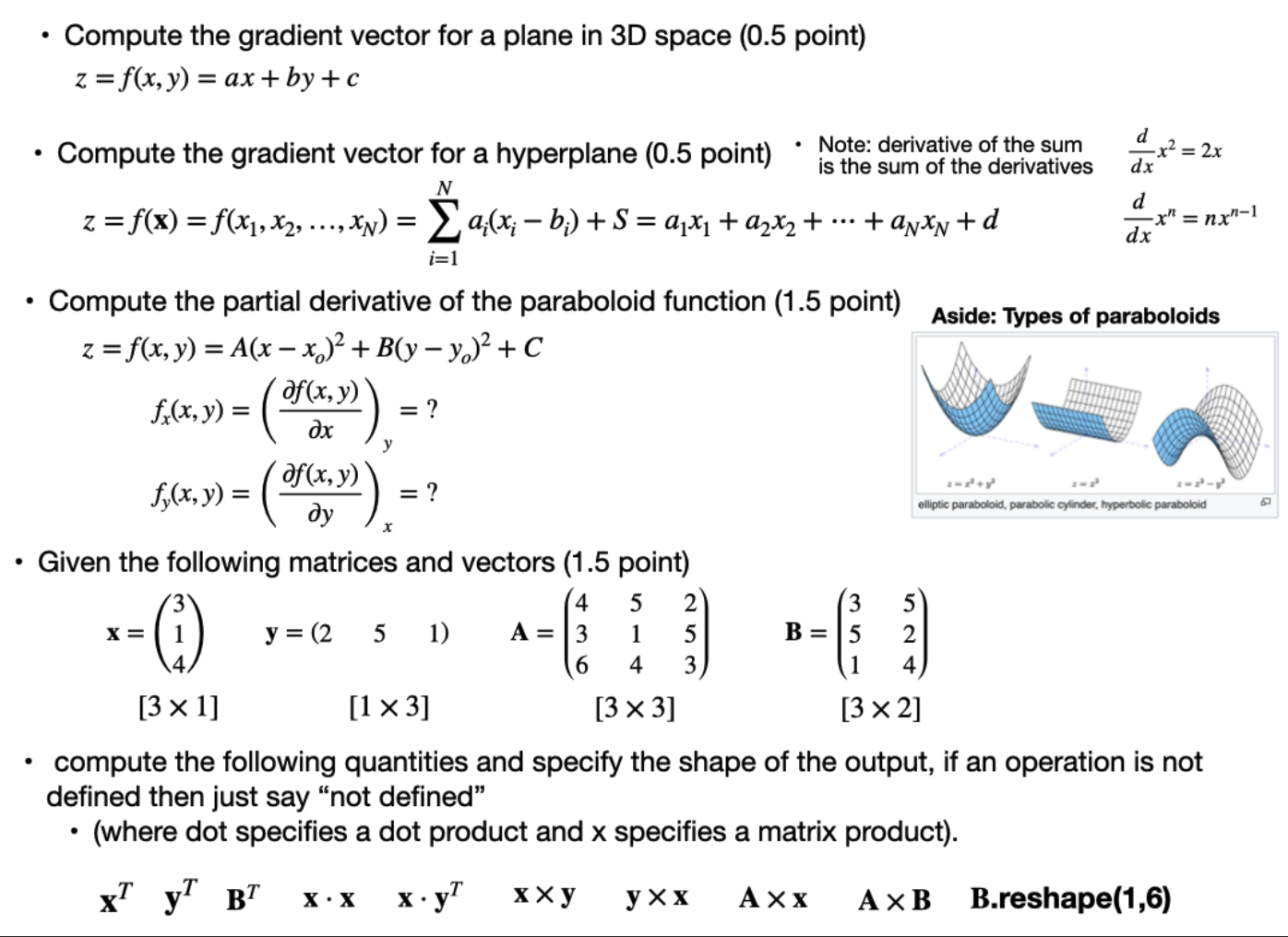
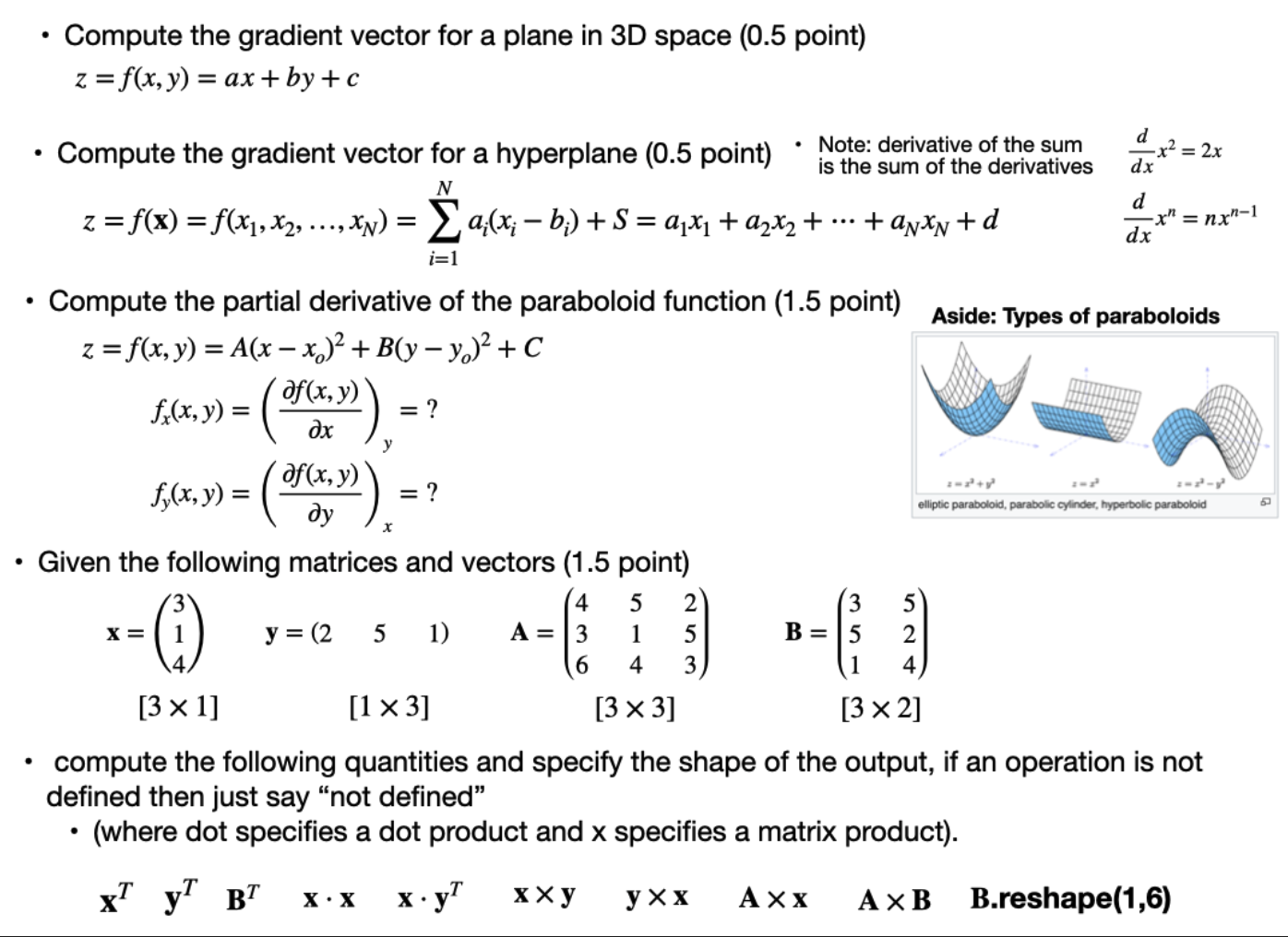
. Compute the gradient vector for a plane in 3D space (0.5 point) z = f(x, y) = ax+ by+ c . Compute the gradient vector for a hyperplane (0.5 point) . Note: derivative of the sum d -x2 = 2x is the sum of the derivatives dx z = f(x) = f(x1, x2, ..., XN) = >a;(x; - b;) + s = ax, + azx2 + ... + axxx+ d d -x" = nx-1 dx i=1 . Compute the partial derivative of the paraboloid function (1.5 point) Aside: Types of paraboloids z = f(x, y) = A(x - x.)2 + B(y - yo)2 + C f.(x, y) = of (x, y) = ? ox f,(x, y) = of (x, y) = ? dy elliptic paraboloid, parabolic cylinder, hyperbolic paraboloid . Given the following matrices and vectors (1.5 point) X= y = (2 5 1 ) A = - UI W WUIN B = AND a w 4 [3 x 1] [1 X 3] [3 x 3] [3 x 2] . compute the following quantities and specify the shape of the output, if an operation is not defined then just say "not defined" . (where dot specifies a dot product and x specifies a matrix product). xT yl BT X . X x. y xXy y X X A X X AXB B.reshape(1,6)Linear least squares (LLS): Single-variable (6 points) - Use Calculus to analytically derive the expression for single variable linear regression fitting parameters using the sum of square error as the loss function (show your work). - That is, do the mathematical optimization problem by hand rather than with a computer N Loss surface: L(p) = L(m, b) = 2 (5'1. Maw, 19))2 P = (Pmpl) = (m,b) i=1 Model: y = M(x| p) = mx + b _ c0v(x,y) _ 1 N 1 _ 2 It : = = i V3I(X)= (xix) so u '0" m var(x) x N Ex N E _ cov(x,y)_ _ 1 N 1 \" _ _ b: _ = I. cov(X,Y)= (xix) i ) y var(x) x y NE); N; (y y Linear least squares (LLS): Multi-variable (EXTRA CREDIT) (+5 points) - Use matrix calculus to analytically derive the expression for two variable linear regression tting parameters using the sum of square error as the loss function - Show your work using matrix notation - From your solution infer the generalized solution for an arbitrary number of variables solution: is = (XTXYIXTY