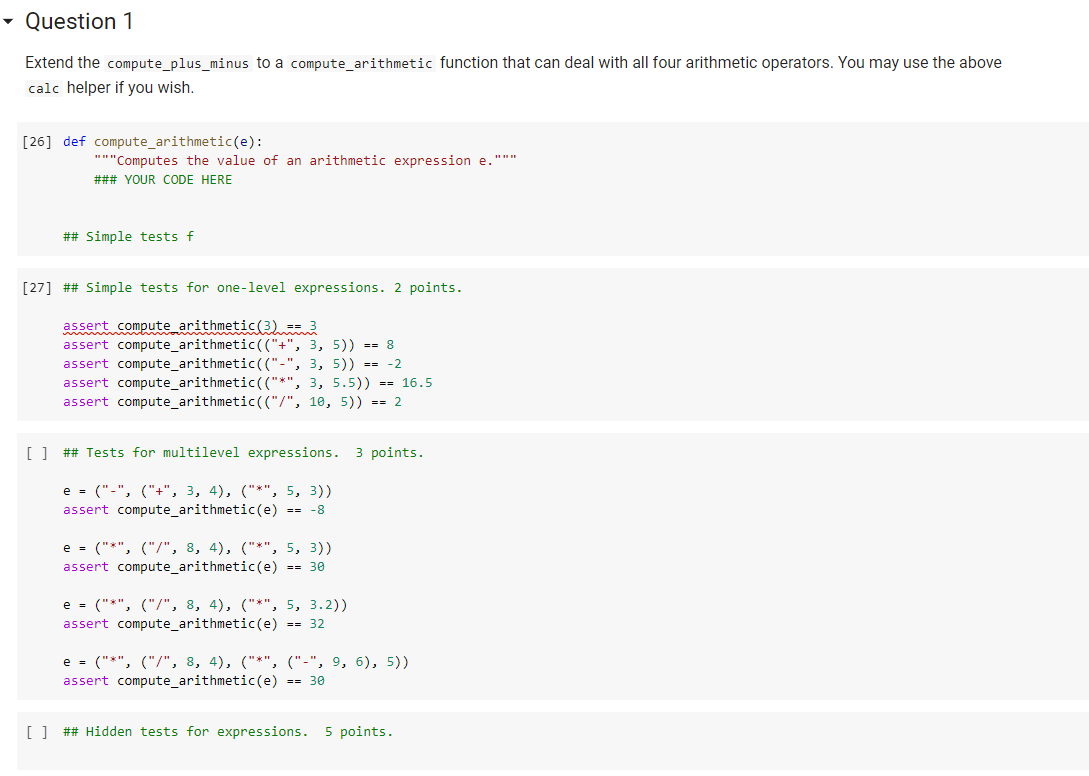
Question: Computer science help please help fill ###Your Code Here Thanks!!! QUESTION 1 def compute_arithmetic(e): Computes the value of an arithmetic expression e. ### YOUR CODE
Computer science help please help fill ###Your Code Here Thanks!!! 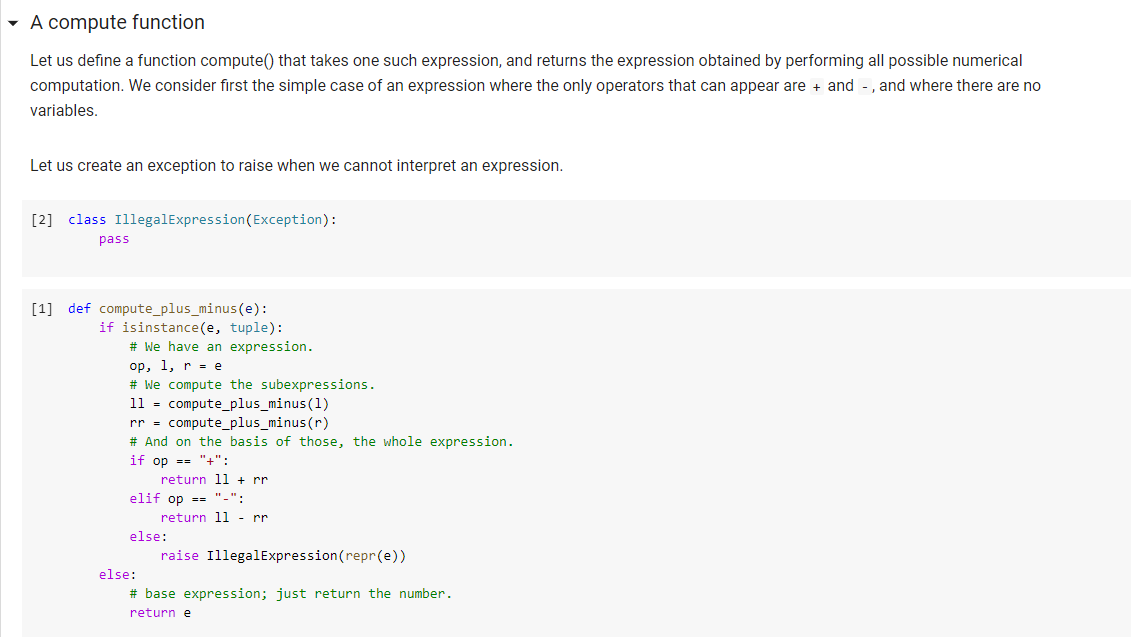
QUESTION 1
def compute_arithmetic(e):
"""Computes the value of an arithmetic expression e."""
### YOUR CODE HERE
## Simple tests f
## Simple tests for one-level expressions. 2 points.
assert compute_arithmetic(3) == 3
assert compute_arithmetic(("+", 3, 5)) == 8
assert compute_arithmetic(("-", 3, 5)) == -2
assert compute_arithmetic(("*", 3, 5.5)) == 16.5
assert compute_arithmetic(("/", 10, 5)) == 2
## Tests for multilevel expressions. 3 points.
e = ("-", ("+", 3, 4), ("*", 5, 3))
assert compute_arithmetic(e) == -8
e = ("*", ("/", 8, 4), ("*", 5, 3))
assert compute_arithmetic(e) == 30
e = ("*", ("/", 8, 4), ("*", 5, 3.2))
assert compute_arithmetic(e) == 32
e = ("*", ("/", 8, 4), ("*", ("-", 9, 6), 5))
assert compute_arithmetic(e) == 30
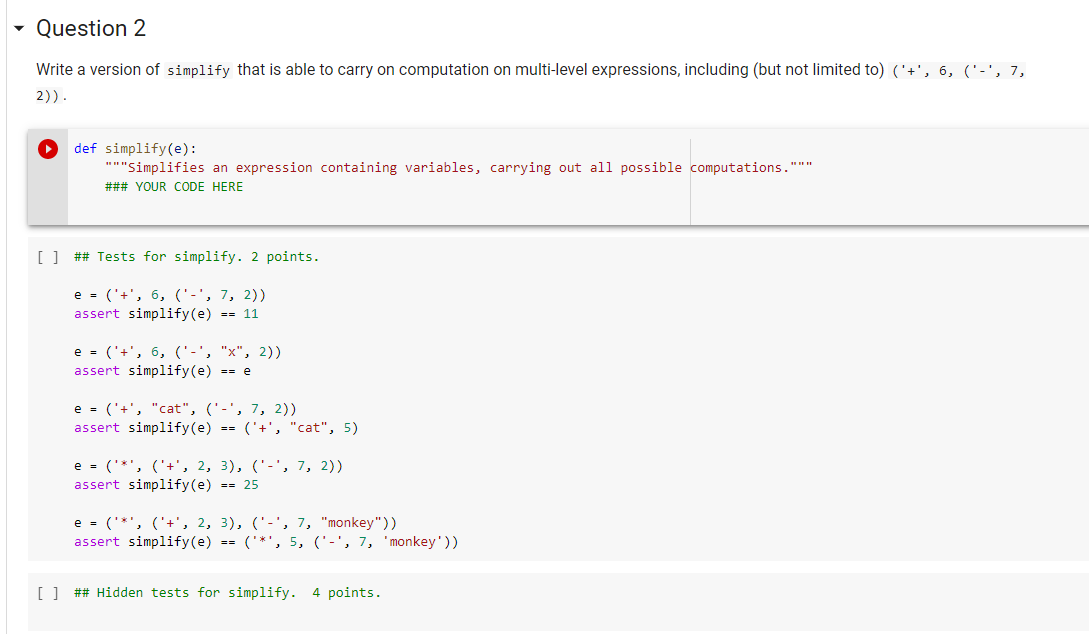
QUESTION 2
def simplify(e):
"""Simplifies an expression containing variables, carrying out all possible computations."""
### YOUR CODE HERE
## Tests for simplify. 2 points.
e = ('+', 6, ('-', 7, 2))
assert simplify(e) == 11
e = ('+', 6, ('-', "x", 2))
assert simplify(e) == e
e = ('+', "cat", ('-', 7, 2))
assert simplify(e) == ('+', "cat", 5)
e = ('*', ('+', 2, 3), ('-', 7, 2))
assert simplify(e) == 25
e = ('*', ('+', 2, 3), ('-', 7, "monkey"))
assert simplify(e) == ('*', 5, ('-', 7, 'monkey'))
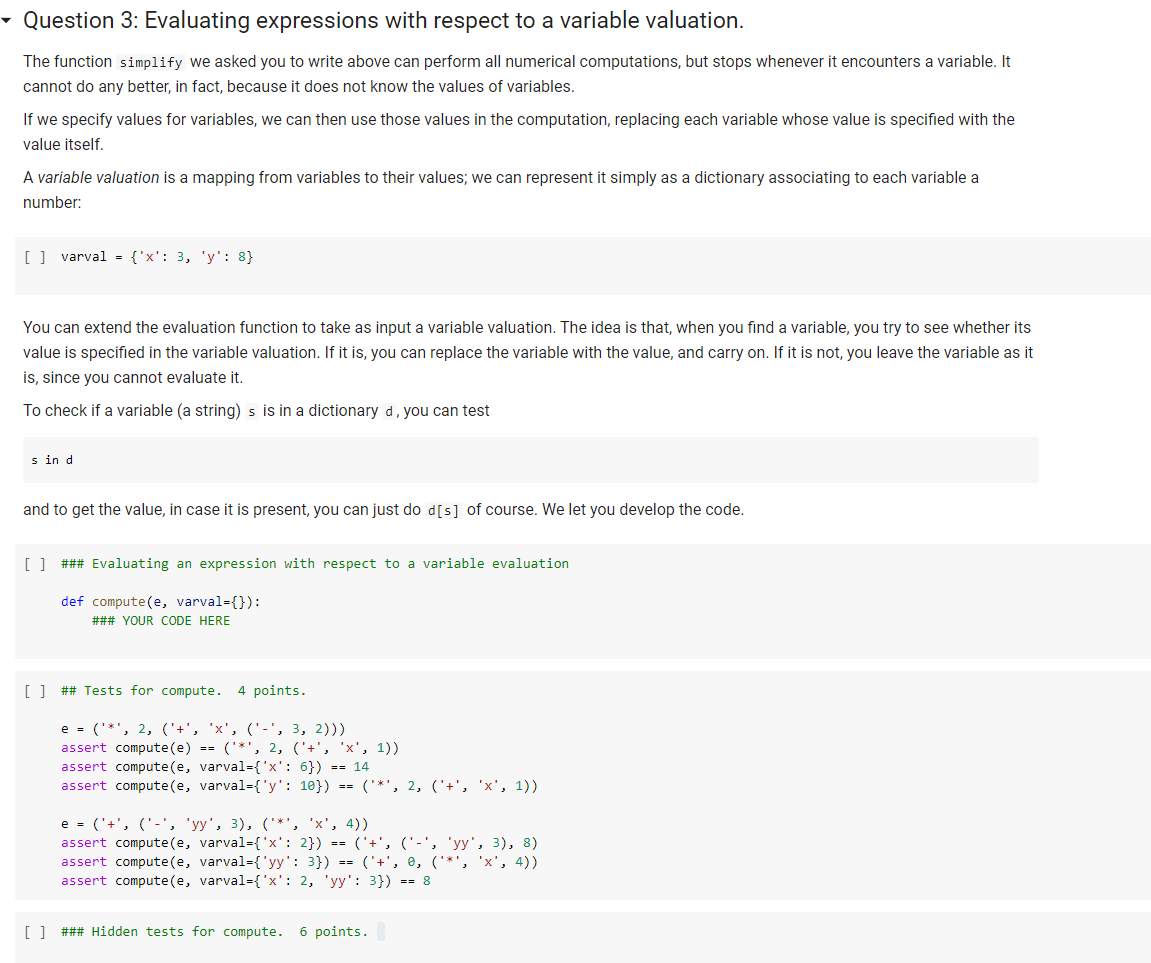
QUESTION 3
### Evaluating an expression with respect to a variable evaluation
def compute(e, varval={}):
### YOUR CODE HERE
## Tests for compute. 4 points.
e = ('*', 2, ('+', 'x', ('-', 3, 2)))
assert compute(e) == ('*', 2, ('+', 'x', 1))
assert compute(e, varval={'x': 6}) == 14
assert compute(e, varval={'y': 10}) == ('*', 2, ('+', 'x', 1))
e = ('+', ('-', 'yy', 3), ('*', 'x', 4))
assert compute(e, varval={'x': 2}) == ('+', ('-', 'yy', 3), 8)
assert compute(e, varval={'yy': 3}) == ('+', 0, ('*', 'x', 4))
assert compute(e, varval={'x': 2, 'yy': 3}) == 8
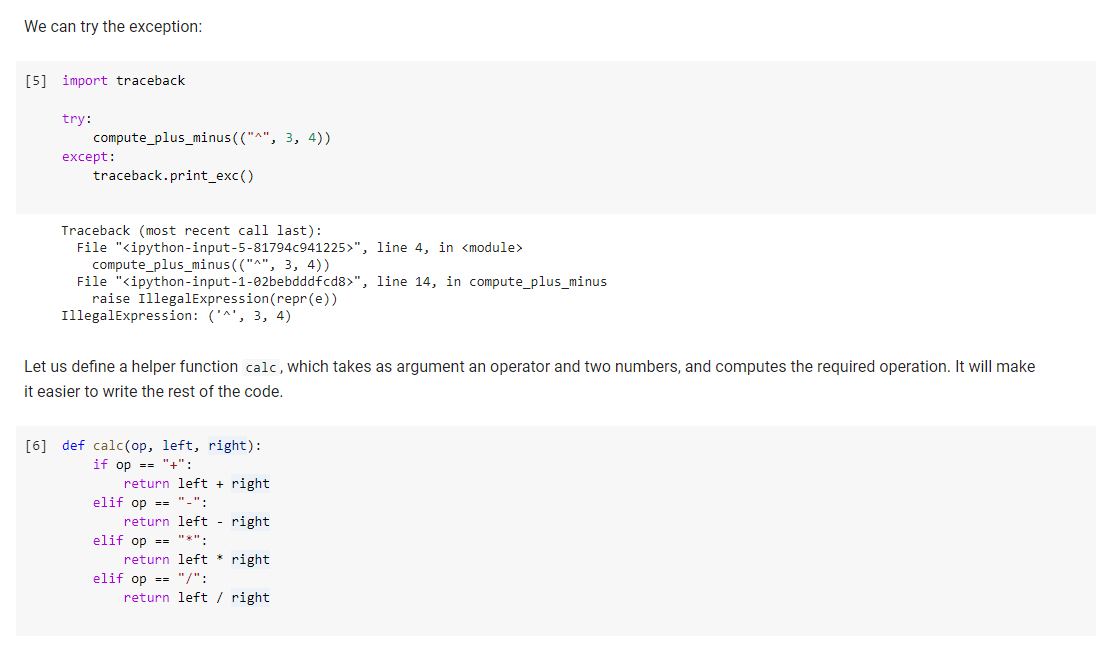
A compute function Let us define a function compute() that takes one such expression, and returns the expression obtained by performing all possible numerical computation. We consider first the simple case of an expression where the only operators that can appear are + and -, and where there are no variables. Let us create an exception to raise when we cannot interpret an expression. [2] class IllegalExpression(Exception): pass [1] def compute_plus_minus(e): if isinstance(e, tuple): # We have an expression. op, l, r = e # We compute the subexpressions. 11 = compute_plus_minus(1) rr = compute_plus_minus(r) # And on the basis of those, the whole expression. if op == "+": return 11 + rr elif op == "-": return ll - rr else: raise IllegalExpression (repr(e)) else: # base expression; just return the number. return e We can try the exception: [5] import traceback try: compute_plus_minus(("A", 3, 4)) except: traceback.print_exc() Traceback (most recent call last): File " compute_plus_minus(("A", 3, 4)) File "", line 14, in compute_plus_minus raise IllegalExpression(repr(e)) IllegalExpression: ("^', 3, 4) Let us define a helper function calc, which takes as argument an operator and two numbers, and computes the required operation. It will make it easier to write the rest of the code. [6] def calc(op, left, right): if op == "+": return left + right elif op == "-": return left - right elif op == "*": return left * right elif op == "/": return left / right Question 1 Extend the compute_plus_minus to a compute_arithmetic function that can deal with all four arithmetic operators. You may use the above calc helper if you wish. [26] def compute_arithmetic(e): """Computes the value of an arithmetic expression e."" ### YOUR CODE HERE ## Simple tests f [27] ## Simple tests for one-level expressions. 2 points. assert compute arithmetic(3) == 3 assert compute_arithmetic(("+", 3, 5)) == 8 assert compute_arithmetic(("-", 3, 5)) == -2 assert compute_arithmetic(("*", 3, 5.5)) == 16.5 assert compute_arithmetic(("/", 10, 5)) == 2 [ ] ## Tests for multilevel expressions. 3 points. e = ("-", ("+", 3, 4), ("*", 5, 3)) assert compute_arithmetic(e) == -8 e = ("*", ("/", 8, 4), ("*", 5, 3)) assert compute_arithmetic(e) == 30 e = ("*", ("/", 8, 4), ("*", 5, 3.2)) assert compute_arithmetic(e) == 32 e = ("*", ("/", 8, 4), ("*", ("-", 9, 6), 5)) assert compute_arithmetic(e) == 30 [] ## Hidden tests for expressions. 5 points. Question 2 ('+', 6, ('-', 7, Write a version of simplify that is able to carry on computation on multi-level expressions, including (but not limited 2)). def simplify(e): ***"Simplifies an expression containing variables, carrying out all possible computations. """ ### YOUR CODE HERE [ ] ## Tests for simplify. 2 points. e = ('+', 6, ('-', 7, 2)) assert simplify() == 11 e = ('+', 6, ('-', "x", 2)) assert simplify(e) == e e = ('+', "cat", ('-', 7, 2)) assert simplify(e) == ('+', "cat", 5) e = ('*', ('+', 2, 3), ('-', 7, 2)) assert simplify(e) == 25 e = ('*', ('+', 2, 3), ('-', 7, "monkey")) assert simplify(e) == (**', 5, ('-', 7, 'monkey')) [ ] ## Hidden tests for simplify. 4 points Question 3: Evaluating expressions with respect to a variable valuation. The function simplify we asked you to write above can perform all numerical computations, but stops whenever it encounters a variable. It cannot do any better, in fact, because it does not know the values of variables. If we specify values for variables, we can then use those values in the computation, replacing each variable whose value is specified with the value itself. A variable valuation is a mapping from variables to their values; we can represent it simply as a dictionary associating to each variable a number: [ ] varval = {'X': 3, 'y': 8} You can extend the evaluation function to take as input a variable valuation. The idea is that, when you find a variable, you try to see whether its value is specified in the variable valuation. If it is, you can replace the variable with the value, and carry on. If it is not, you leave the variable as it is, since you cannot evaluate it. To check if a variable (a string) s is in a dictionary d, you can test s in d and to get the value, in case it is present, you can just do d[s] of course. We let you develop the code. [] ### Evaluating an expression with respect to a variable evaluation def compute(e, varval={}): ### YOUR CODE HERE [] ## Tests for compute. 4 points e = ('*', 2, ('+', 'x', ('-', 3, 2))) assert compute(e) == ('*', 2, ('+', 'x', 1)) assert compute(e, varval={'X': 6]) == 14 assert compute(e, varval={'y': 10}) == (**', 2, ('+', 'x', 1)) e = ('+', ('-', 'y', 3), ("*', 'x', 4)) assert compute(e, varval={'X': 2}) == ('+', ('-', 'yy', 3), 8) assert compute(e, varval={'yy': 3}) == ('+', 0, ("*', 'x', 4)) assert compute(e, varval={'X': 2, 'yy': 3}) == 8 [ ] ### Hidden tests for compute. 6 points. A compute function Let us define a function compute() that takes one such expression, and returns the expression obtained by performing all possible numerical computation. We consider first the simple case of an expression where the only operators that can appear are + and -, and where there are no variables. Let us create an exception to raise when we cannot interpret an expression. [2] class IllegalExpression(Exception): pass [1] def compute_plus_minus(e): if isinstance(e, tuple): # We have an expression. op, l, r = e # We compute the subexpressions. 11 = compute_plus_minus(1) rr = compute_plus_minus(r) # And on the basis of those, the whole expression. if op == "+": return 11 + rr elif op == "-": return ll - rr else: raise IllegalExpression (repr(e)) else: # base expression; just return the number. return e We can try the exception: [5] import traceback try: compute_plus_minus(("A", 3, 4)) except: traceback.print_exc() Traceback (most recent call last): File " compute_plus_minus(("A", 3, 4)) File "", line 14, in compute_plus_minus raise IllegalExpression(repr(e)) IllegalExpression: ("^', 3, 4) Let us define a helper function calc, which takes as argument an operator and two numbers, and computes the required operation. It will make it easier to write the rest of the code. [6] def calc(op, left, right): if op == "+": return left + right elif op == "-": return left - right elif op == "*": return left * right elif op == "/": return left / right Question 1 Extend the compute_plus_minus to a compute_arithmetic function that can deal with all four arithmetic operators. You may use the above calc helper if you wish. [26] def compute_arithmetic(e): """Computes the value of an arithmetic expression e."" ### YOUR CODE HERE ## Simple tests f [27] ## Simple tests for one-level expressions. 2 points. assert compute arithmetic(3) == 3 assert compute_arithmetic(("+", 3, 5)) == 8 assert compute_arithmetic(("-", 3, 5)) == -2 assert compute_arithmetic(("*", 3, 5.5)) == 16.5 assert compute_arithmetic(("/", 10, 5)) == 2 [ ] ## Tests for multilevel expressions. 3 points. e = ("-", ("+", 3, 4), ("*", 5, 3)) assert compute_arithmetic(e) == -8 e = ("*", ("/", 8, 4), ("*", 5, 3)) assert compute_arithmetic(e) == 30 e = ("*", ("/", 8, 4), ("*", 5, 3.2)) assert compute_arithmetic(e) == 32 e = ("*", ("/", 8, 4), ("*", ("-", 9, 6), 5)) assert compute_arithmetic(e) == 30 [] ## Hidden tests for expressions. 5 points. Question 2 ('+', 6, ('-', 7, Write a version of simplify that is able to carry on computation on multi-level expressions, including (but not limited 2)). def simplify(e): ***"Simplifies an expression containing variables, carrying out all possible computations. """ ### YOUR CODE HERE [ ] ## Tests for simplify. 2 points. e = ('+', 6, ('-', 7, 2)) assert simplify() == 11 e = ('+', 6, ('-', "x", 2)) assert simplify(e) == e e = ('+', "cat", ('-', 7, 2)) assert simplify(e) == ('+', "cat", 5) e = ('*', ('+', 2, 3), ('-', 7, 2)) assert simplify(e) == 25 e = ('*', ('+', 2, 3), ('-', 7, "monkey")) assert simplify(e) == (**', 5, ('-', 7, 'monkey')) [ ] ## Hidden tests for simplify. 4 points Question 3: Evaluating expressions with respect to a variable valuation. The function simplify we asked you to write above can perform all numerical computations, but stops whenever it encounters a variable. It cannot do any better, in fact, because it does not know the values of variables. If we specify values for variables, we can then use those values in the computation, replacing each variable whose value is specified with the value itself. A variable valuation is a mapping from variables to their values; we can represent it simply as a dictionary associating to each variable a number: [ ] varval = {'X': 3, 'y': 8} You can extend the evaluation function to take as input a variable valuation. The idea is that, when you find a variable, you try to see whether its value is specified in the variable valuation. If it is, you can replace the variable with the value, and carry on. If it is not, you leave the variable as it is, since you cannot evaluate it. To check if a variable (a string) s is in a dictionary d, you can test s in d and to get the value, in case it is present, you can just do d[s] of course. We let you develop the code. [] ### Evaluating an expression with respect to a variable evaluation def compute(e, varval={}): ### YOUR CODE HERE [] ## Tests for compute. 4 points e = ('*', 2, ('+', 'x', ('-', 3, 2))) assert compute(e) == ('*', 2, ('+', 'x', 1)) assert compute(e, varval={'X': 6]) == 14 assert compute(e, varval={'y': 10}) == (**', 2, ('+', 'x', 1)) e = ('+', ('-', 'y', 3), ("*', 'x', 4)) assert compute(e, varval={'X': 2}) == ('+', ('-', 'yy', 3), 8) assert compute(e, varval={'yy': 3}) == ('+', 0, ("*', 'x', 4)) assert compute(e, varval={'X': 2, 'yy': 3}) == 8 [ ] ### Hidden tests for compute. 6 points








