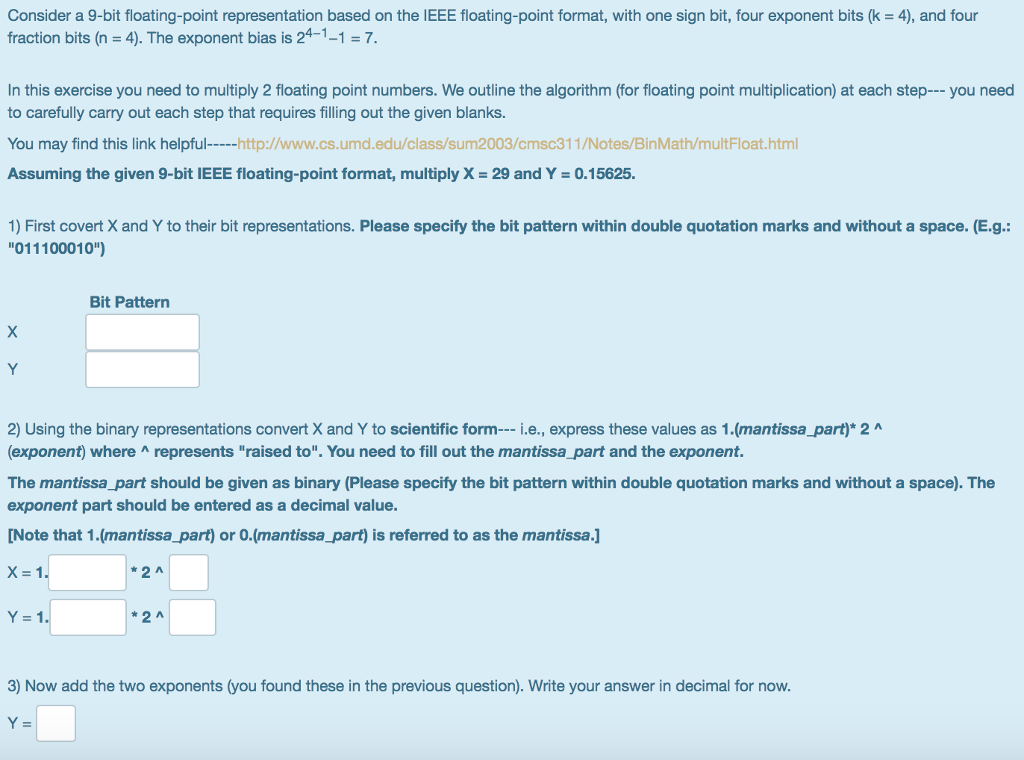
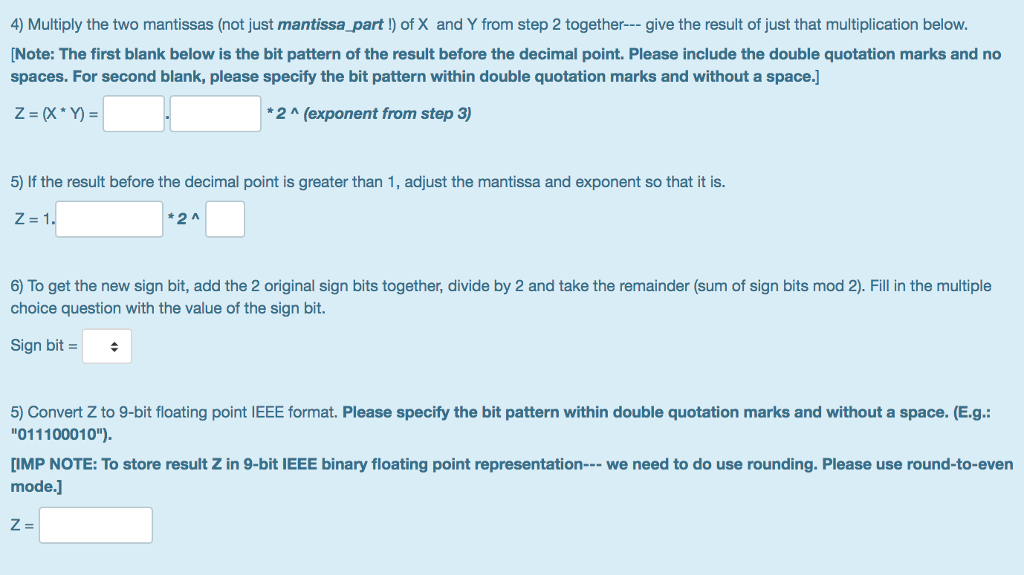
Consider a 9-bit floating-point representation based on the IEEE floating-point format, with one sign bit, four exponent bits (k-4), and four fraction bits (n = 4). The exponent bias is 24-1-1-7. In this exercise you need to multiply 2 floating point numbers. We outline the algorithm (for floating point multiplication) at each step-you need to carefully carry out each step that requires filling out the given blanks. You may find this link helpful--http://www.cs.umd.edu/class/sum2003/cmsc31 1/Notes/BinMath/multFloat.html Assuming the given 9-bit IEEE floating-point format, multiply X = 29 and Y = 0.15625. 1) First covert X and Y to their bit representations. Please specify the bit pattern within double quotation marks and without a space. (E.g.: 011100010") Bit Pattern 2) Using the binary representations convert X and Y to scientific form i.e., express these values as 1.(mantissa_part)* 2 (exponent) where A represents "raised to". You need to fill out the mantissa_part and the exponent. The mantissa_part should be given as binary (Please specify the bit pattern within double quotation marks and without a space). The exponent part should be entered as a decimal value. Note that 1.(mantissa_part) or O.(mantissa_part) is referred to as the mantissa.] 2 A Y=1. 2 A 3) Now add the two exponents (you found these in the previous question). Write your answer in decimal for now Y=