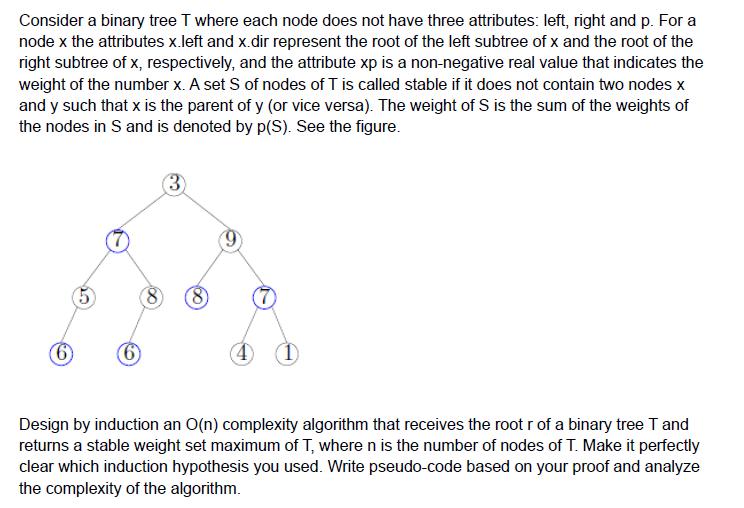
Consider a binary tree T where each node does not have three attributes: left, right and p. For a node x the attributes x.left and x.dir represent the root of the left subtree of x and the root of the right subtree of x, respectively, and the attribute xp is a non-negative real value that indicates the weight of the number x. A set S of nodes of T is called stable if it does not contain two nodes x and y such that x is the parent of y (or vice versa). The weight of S is the sum of the weights of the nodes in S and is denoted by p(S). See the figure. (6) (6) 3 (8) Design by induction an O(n) complexity algorithm that receives the root r of a binary tree T and returns a stable weight set maximum of T, where n is the number of nodes of T. Make it perfectly clear which induction hypothesis you used. Write pseudo-code based on your proof and analyze the complexity of the algorithm.