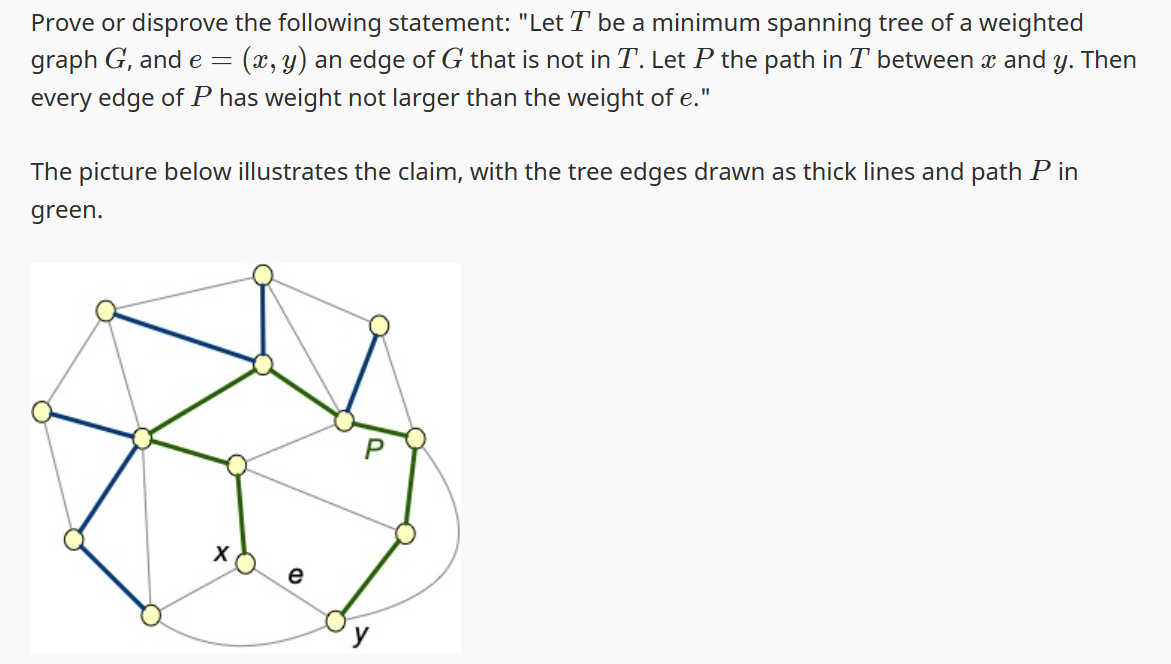
Consider a connected graph G with 15 vertices, that contains two cycles of length 3 that do not share any vertices, both cycles consisting of edges with weight 5 , and all other edges in G have weight 8 . What is the minimum weight of a spanning tree of G ? Prove or disprove the following statement: "Let T be a minimum spanning tree of a weighted graph G, and e=(x,y) an edge of G that is not in T. Let P the path in T between x and y. Then every edge of P has weight not larger than the weight of e." The picture below illustrates the claim, with the tree edges drawn as thick lines and path P in green