Question: Consider a discrete-time system described by: where x(k), x2(k) and xz(k) are the states and u(k) is the input. Find the necessary and sufficient conditions

Consider a discrete-time system described by:

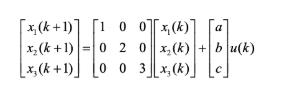
Consider a discrete-time system described by: where x(k), x2(k) and xz(k) are

where x(k), x2(k) and xz(k) are the states and u(k) is the input. Find the necessary and sufficient conditions on a, b, and c so that the system is controllable. Justify your answer.

Step by Step Solution

★★★★★

3.33 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To determine the controllability of the given discretetime system we need to examine the controllability matrix and ensure it has full rank The systems statespace representation is xk1 Axk Buk Where A beginbmatrix 1 0 0 0 2 0 0 0 3 endbmatrix quad B beginbmatrix a b c endbmatrix Step 1 Controllability Matrix The controllability matrix C is given by C beginbmatrix B AB A2B endbmatrix Step 2 Compute AB AB A cdot B beginbmatrix 1 0 0 0 2 0 0 0 3 endbmatrix beginbmatrix a b c endbmatrix beginbmatrix a 2b 3c endbmatrix Step 3 Compute A2B A2 A cdot A beginbmatrix 1 0 0 0 2 0 0 0 3 endbmatrix beginbmatrix 1 0 0 0 2 0 0 0 3 endbmatrix beginbmatrix 1 0 0 0 4 0 0 0 9 endbmatrix A2B A2 cdot B beginbmatrix 1 0 0 0 4 0 0 0 9 endbmatrix beginbmatrix a b c endbmatrix beginbmatrix a 4b 9c endbmatrix Step 4 Construct the Controllability Matrix C beginbmatrix B AB A2B endbmatrix beginbmatrix a a a b 2b 4b c 3c 9c endbmatrix Step 5 Determine the Rank of C The system ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Electrical Engineering Questions!

Consider the system described by where x(t) = [x1(t) x2(t)]T. (a) Compute the state transition matrix (t, 0). 0 2 3x()

Let (i). Write down necessary and sufficient conditions on the entries a, b, c, d that ensures that A has only real eigenvalues. (ii).Verify that all symmetric 2 2 matrices satisfy your conditions....

Let (a) Write down necessary and sufficient conditions on the entries a, b, c, d that ensures that A has only real eigenvalues. (b) Verify that all symmetric 2 Ã 2 matrices satisfy your...

(i) Write down the linear program relaxation for the vertex cover problem and solve the linear program. [6 marks] (ii) Based on the solution of the linear program in (b)(i), derive an integer...

Prolog You are approached to compose a Prolog program to work with twofold trees. Your code shouldn't depend on any library predicates and you ought to expect that the mediator is running without...

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

In this simulation-based assignment, you will utilize MATLAB to implement two different procedures for mobile robot simultaneous localization and mapping (SLAM) in discrete time, utilizing both...

N A S TIO I C VE A N T I IZ O E T N R C A TI O PE G CA E S R NI H R T E O U P OR M 2 F OM E R T P C A L C H A L LEARNING OBJECTIVES After studying this chapter, you will be able to answer several...

Let r and s be solutions to the quadratic equation x 2 b x + c = 0. For n N, define d0 = 0 d1 = r s dn = b dn1 c dn2 (n 2) Prove that dn = r n s n for all n N. [4 marks] (b) Recall that a commutative...

Edgerron Company is able to produce two products, G and B, with the same machine in its factory. The following information is available. Product G- Produot 3 Selling price per unit $ 150 $ 150...

ANOVA CASE STUDY The watch supervisor wants to know if there is a statistical significance between the working shift's productivity. The following data pertains: 4 PMMidnight 21 Midnight 8 AM...

the McKinsey Customer Decision Journey model of consumer behavior suggests that the best thing fter customers make a purchase is: Begin an ongoing and regular process of exposing them to the brand\'s...

B Remember to SAVE your work C D QUESTION 3-REVENUE VARIANCE ANALYSIS-Version C (25 marks) ABC Co. manufactures widgets and has the following operating Information for the past year: Product Line...

5. Use any method (including calculators!) to compute the following volumes. a) The region bounded by y = sin(x) and the lines y = 0, x = 0, and x = 2 rotated around the x-axis. b) The region bounded...

solve this problem by showing the manual calculation and choose the correct answer(mechanical vibrations) Find the natural frequencies of the system for k = 300 N/m, k2 = 500 N/m, k3 = 200 N/m, m = 2...

Shown below is an income statement for 2016 that was prepared by a poorly trained bookkeeper of Howell Corporation. Howell Corporation INCOME STATEMENT December 31, 2016 Sales revenue $945,000...

You have just begun your summer internship at Omni Instruments. The company supplies sterilized surgical instruments for physicians. To expand sales, Omni is considering paying a commission to its...

In problem, convert each angle to DM ' S '' form. Round your answer to the nearest second. 19.99

Plot each point given in polar coordinates, and find its rectangular coordinates. (-4,- /4)

The end of a tuning fork moves in simple harmonic motion described by the equation d = a sin (t). If a tuning fork for the note E above middle C on an even-tempered scale (E 4 ) has a frequency of...

This problem demonstrates the dramatic effect that consolidation accounting can have on a company's ratios. Randall Motor Company (Randall) owns 100% of Randall Motor Credit Corporation (RMCC), its...

The Cola Company reported the following comparative information at December 31, 2017, and December 31, 2016 (amounts in millions and adapted): Requirements 1. Calculate the following ratios for 2017...

Financial institutions hold large quantities of bond investments. Suppose Sun Life Financial purchases $500,000 of 6% bonds of General Components Corporation for 88 on January 1, 2017, when the...