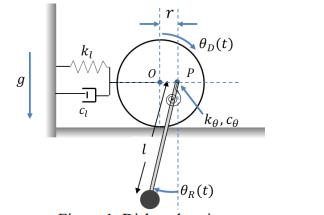
Consider a disk with mass M, radius R, and moment of inertia ID (about its center, point O) rolling without slipping on a horizontal surface as shown in Figure 1 below. The disk is connected to a linear spring of stiffness kl and damper cl at point O. Additionally, the disk is connected to a rigid, massless rod, of length I with a mass m at the end, through a torsional spring ke and damper ce at point P. Point P is offset from the center of the disk by a distance r. You may assume that the angle D is small, but the angle R is not small. Gravity acts downward as shown. Complete the following: (a) How many generalized coordinates are required for this problem? (b) Using Lagrange's Equations, derive the equations of motion for the system. g k 0 L 100 (t) P ke, Ce -On(t)