Consider a linear programming problem shown below, given in standard form with dual variables associated with each constraint in red beside the constraints.

Max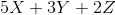

s.t.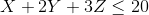

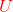
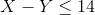
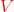
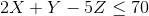
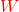
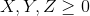
Part 1: Write the dual objective function. Is it minimization or maximization?

Part 2: Write the dual constraints. Clearly state conditions on the dual variables.

Part 3: An optimal solution will satisfy all of the following conditions: 1) all primal constraints are satisfied, 2) all dual constraints are satisfied, 3) the primal and dual objective functions must be equal. For each of the 4 following possible solutions to the problem, identify whether or not it is optimal and give at least one reason why it is/is not optimal. Only one solution is optimal.

Solution 1: X = 17, Y = 0, Z = 1, U = 1.55, V = 4, W = 0; Solution 2: X = 16, Y = 2, Z = 0, U = 2.667, V = 2.333, W = 0; Solution 3: X = 15, Y = 3, Z = 1, U = 2, V = 4, W = 0; Solution 4: X = 19, Y = 1, Z = 1, U = 1.5, V = 0, W = 1.

Transcribed image text