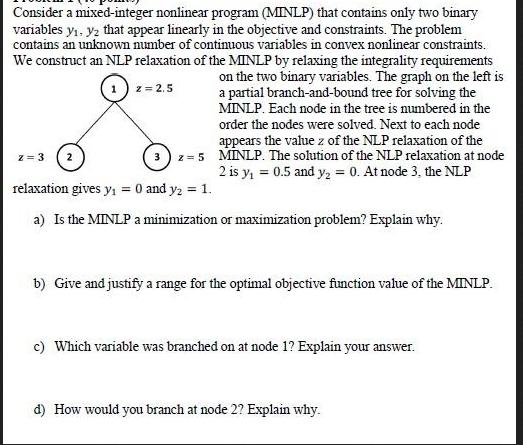
Consider a mixed-integer nonlinear program (MINLP) that contains only two binary variables y, y that appear linearly in the objective and constraints. The problem contains an unknown number of continuous variables in convex nonlinear constraints. We construct an NLP relaxation of the MINLP by relaxing the integrality requirements z = 2.5 on the two binary variables. The graph on the left is a partial branch-and-bound tree for solving the MINLP. Each node in the tree is numbered in the order the nodes were solved. Next to each node appears the value z of the NLP relaxation of the z = 5 MINLP. The solution of the NLP relaxation at node 2 is y = 0.5 and y = 0. At node 3, the NLP z = 3 relaxation gives y = 0 and y2 = 1. a) Is the MINLP a minimization or maximization problem? Explain why. b) Give and justify a range for the optimal objective function value of the MINLP. c) Which variable was branched on at node 1? Explain your answer. d) How would you branch at node 2? Explain why.