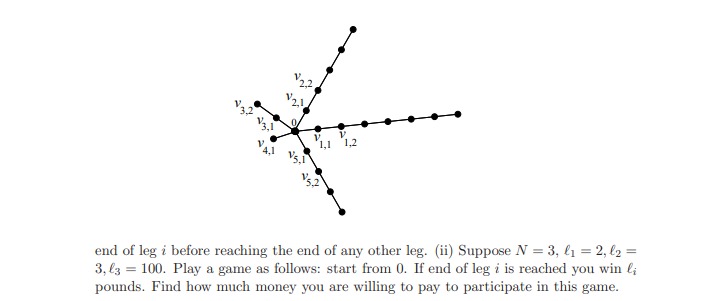
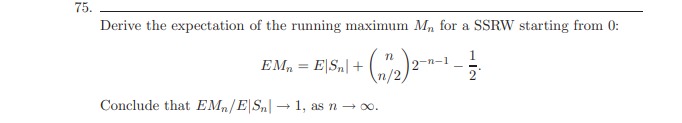Question: Consider a random walk on a star-graph that has one centre vertex ( and /V legs emanating from 0. Leg i contains &; vertices (in
Consider a random walk on a star-graph that has one centre vertex ( and /V legs emanating from 0. Leg i contains &; vertices (in addition to () labelled Vi, 1, Vi,2, . . . , Vi,&,- The vertices are in sequence: 0 is connected to vij which is connected to vi2, etc. till the end vertex vie. (i) A particle starts at 0. Find the probability that it reaches the2,2 V V21 3.2 V4.1 V 1,1 1,2 4.1 Va 2 end of leg i before reaching the end of any other leg. (ii) Suppose N = 3, 61 = 2, (2 = 3, 63 = 100. Play a game as follows: start from 0. If end of leg i is reached you win l; pounds. Find how much money you are willing to pay to participate in this game.98. There are / coloured items. There are c possible colours. Pick an items at random and change its colour to one of the other c - 1 colours at random. Keep doing this. What is the Markov chain describing this experiment? Find its stationary distribution. (Hint: When c = 2 it is the Ehrenfest chain.)94. Simple queueing system: Someone arrives at a bank at time n with probability ox. He or she waits in a queue {if any} which is served by one bank clerk in a FCFS fashion. 'When at the head of the queue. the person requires a service which is distributed like a random variable 5' with values in H: P{S = 1:} = pm It = 11 2, .. .. Different people require services which are independent random variables. Consider the quantity W}, which is the total waiting time at time n: if I take a look at the queue at time n then W\" represents the time I have to wait in line till I nish my service. {i} Show that Wn obeys the recursion I'il:"rr':+2i = {WI-J. + 311611 1):}? where the 5,. are i.i.d. random variables distributed like 3: independent of the E\". The latter are also i.i.d. with PE\" = 1] = or, PE\" = } = 1 or. Thus in = 1 indicates that there is an arrival at time #1. {ii} Show that Wu is a Markov chain and compute its transition probabilities me, E]? tel? = lll,,1.,2,...1 in terms of the parameters or and pk. {iii} Suppose that p1 = l ,3, p2 = .3. Find conditions on o: and g3 so that the stationary distribution exists. [iv] lGive a physical interpretation of this condition. [v] Find the stationary distribution. {vi} Find the average waiting time in steady-state. (vii) If :1 = 4ft: [-1 customers arrive every 5 units of time on the averageheavy trafc)1 what is the maximum value of .13 so that a stationary distribution exists? What is the average waitine: time when H = H.242\" 93. Build a Markov chain as follows: When in state k (k = 1, 2, 3, 4, 5,6), roll a die & times, take the largest value and move to that state. (i) Compute the transition probabilities and write down the transition probability matrix. (ii) Is the chain aperiodic? (iii) Does it have a unique stationary distribution? (iv) Can you find which state will be visited more frequently on the average?75. Derive the expectation of the running maximum M, for a SSRW starting from 0: EMn = ElSal+ (12/2)2-1. Conclude that EM,/ E|S,| - 1, as n - 00.73. Consider a SIMPLE SYMMETRIC RANDOM WALK starting from 0 and let T, be the first time that state a will be visited. Derive the formulae for P(T,