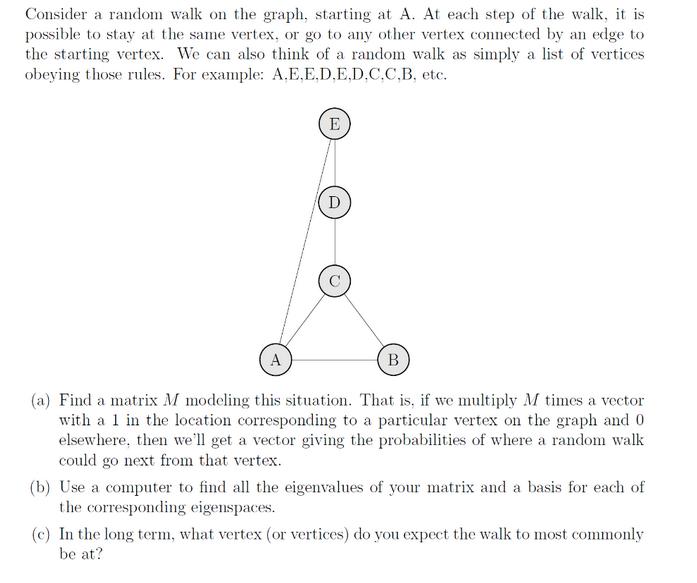
Consider a random walk on the graph, starting at A. At each step of the walk, it is possible to stay at the same vertex, or go to any other vertex connected by an edge to the starting vertex. We can also think of a random walk as simply a list of vertices obeying those rules. For example: A.E.E.D.E.D.C.C.B. etc. A E D B (a) Find a matrix M modeling this situation. That is, if we multiply M times a vector with a 1 in the location corresponding to a particular vertex on the graph and 0 elsewhere, then we'll get a vector giving the probabilities of where a random walk could go next from that vertex. (b) Use a computer to find all the eigenvalues of your matrix and a basis for each of the corresponding eigenspaces. (c) In the long term, what vertex (or vertices) do you expect the walk to most commonly be at?