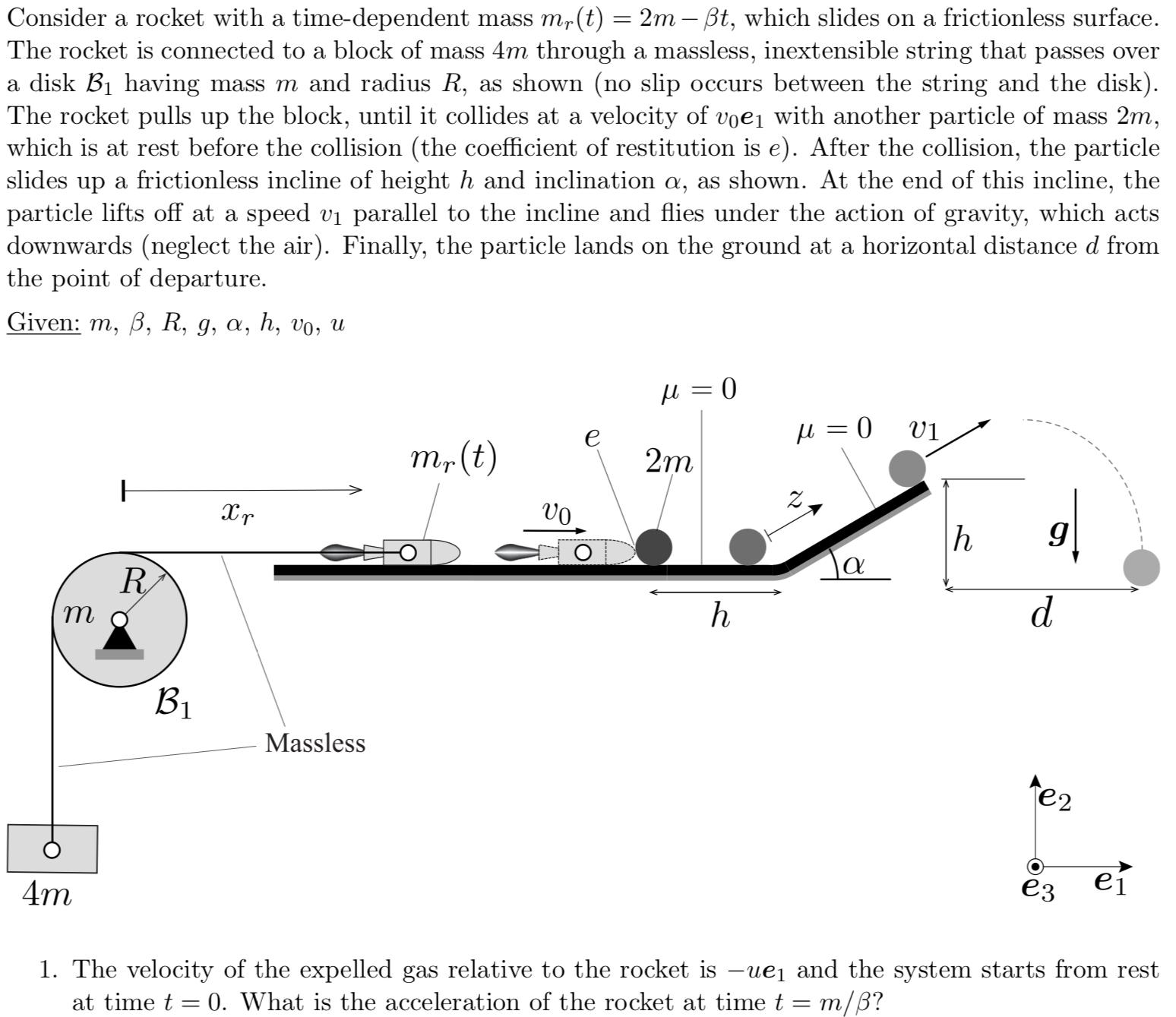
Consider a rocket with a time-dependent mass mr(t) = 2m - t, which slides on a frictionless surface. The rocket is connected to a block of mass 4m through a massless, inextensible string that passes over a disk B having mass m and radius R, as shown (no slip occurs between the string and the disk). The rocket pulls up the block, until it collides at a velocity of voe with another particle of mass 2m, which is at rest before the collision (the coefficient of restitution is e). After the collision, the particle slides up a frictionless incline of height h and inclination a, as shown. At the end of this incline, the particle lifts off at a speed v parallel to the incline and flies under the action of gravity, which acts downwards (neglect the air). Finally, the particle lands on the ground at a horizontal distance d from the point of departure. Given: m, , R, g, a, h, vo, u m 4m R B Xr Massless mr(t) U0 = 0 2m h =0 01 Z h 9 d tez e3 e 1. The velocity of the expelled gas relative to the rocket is -ue and the system starts from rest at time t = 0. What is the acceleration of the rocket at time t = m/?