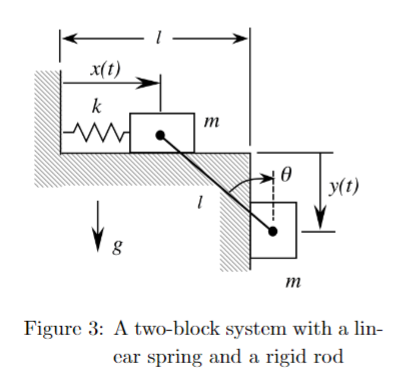
Consider a two$-$block system moving in the gravity field shown in Fig. $3.$Figure $3$: A two$-$block system with a lin$-$

ear spring and a rigid rod

The two blocks have the same mass $m$ and are connected via a rigid, massless rod of length $l.$

As a result of the gravitational acceleration $g,$ block $1$ moves horizontally and block $2$ can only

move vertically. There is no friction in this system. Moreover, block $1$ is connected to a wall

via a linear spring that has a spring constant $k$ and a negligible free length. Therefore, the

elongation of the spring is the position $x$ of block $1$ from the wall. For block $2,$ its horizontal

distance to the wall is $l$ and its vertical position is $y$ as shown in Fig. $3.$ Use Newtonian

mechanics to answer the following questions.

$($a$)$ Draw a free$-$body diagram of the two blocks.

$($b$)$ Apply Newton's second law to derive the equations of motion of the two blocks. Elimi$-$

nate constraint force$($s$)$ from your equations of motion to obtain a nonlinear, differential

equation governing only the variable $(t),$ where $$ is the angle between the rigid rod and

the vertical as shown in Fig. $3.$

$($c$)$ Determine an algebraic equation governing equilibrium positions ${}_0$ of the system. The

equation should involve parameters such as mg and kl $.$ Show that there is only one

possible equilibrium for

$($d$)$ Derive a linearized equation of motion around the equilibrium position. If the two$-$block

system is subjected to disturbance, will the system oscillate around the equilibrium

position? Why?