Consider a two-period binomial model in which a stock currently priced at $65. In the next period, the stock can either increase by 20 percent or decrease by 17 percent. Assume a European call option with an exercise price of $60 and the risk-free rate of 5 percent. Assume that you can long and short US Treasury securities (equivalently, you can lend and borrow money at the risk-free interest rate). Also, the stock does not pay any dividend over the life of the option.

1) (10pts) Calculate the price of the call option (X=60). You may solve this problem by completing the cells in gray. Fill out information with equations.

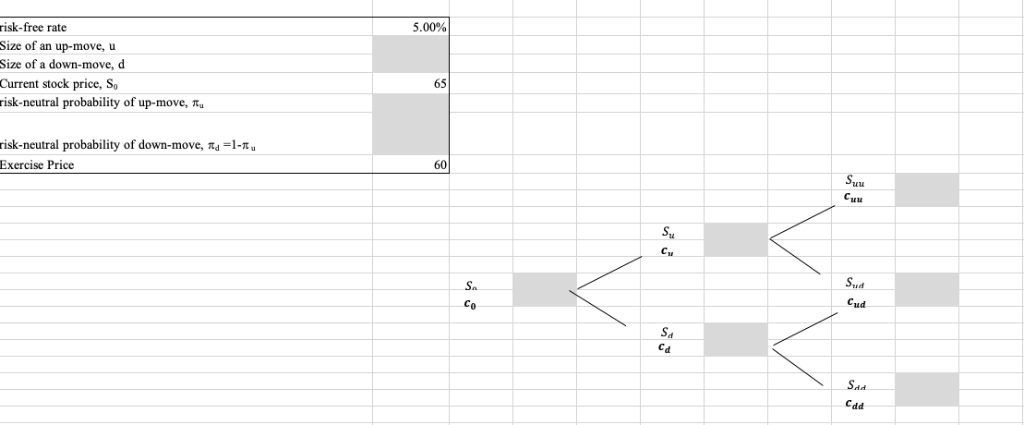
2) (15pts) Based on your answer in Part 1), calculate the number of units of the underlying stock that would be needed at eah point in the binomial tree to construct a risk-free hedge. Use 100 calls (one contract). in other words, you need to find the unit of the underlyng stocks for a risk-free hedge portfolio at t=0 when the stock price is $65, the unit of the underlyng stocks at t=1 when the stock price ends up with Su , the unit of the underlyng stocks at t=1 when the stock price ends up with Sd . Fill out grey cells with equations.

Hedge ratio at t-0 Hedge ratio when the stock price is up at t-1, S, Hedge ratio when the stock price is down at t-1, Sd