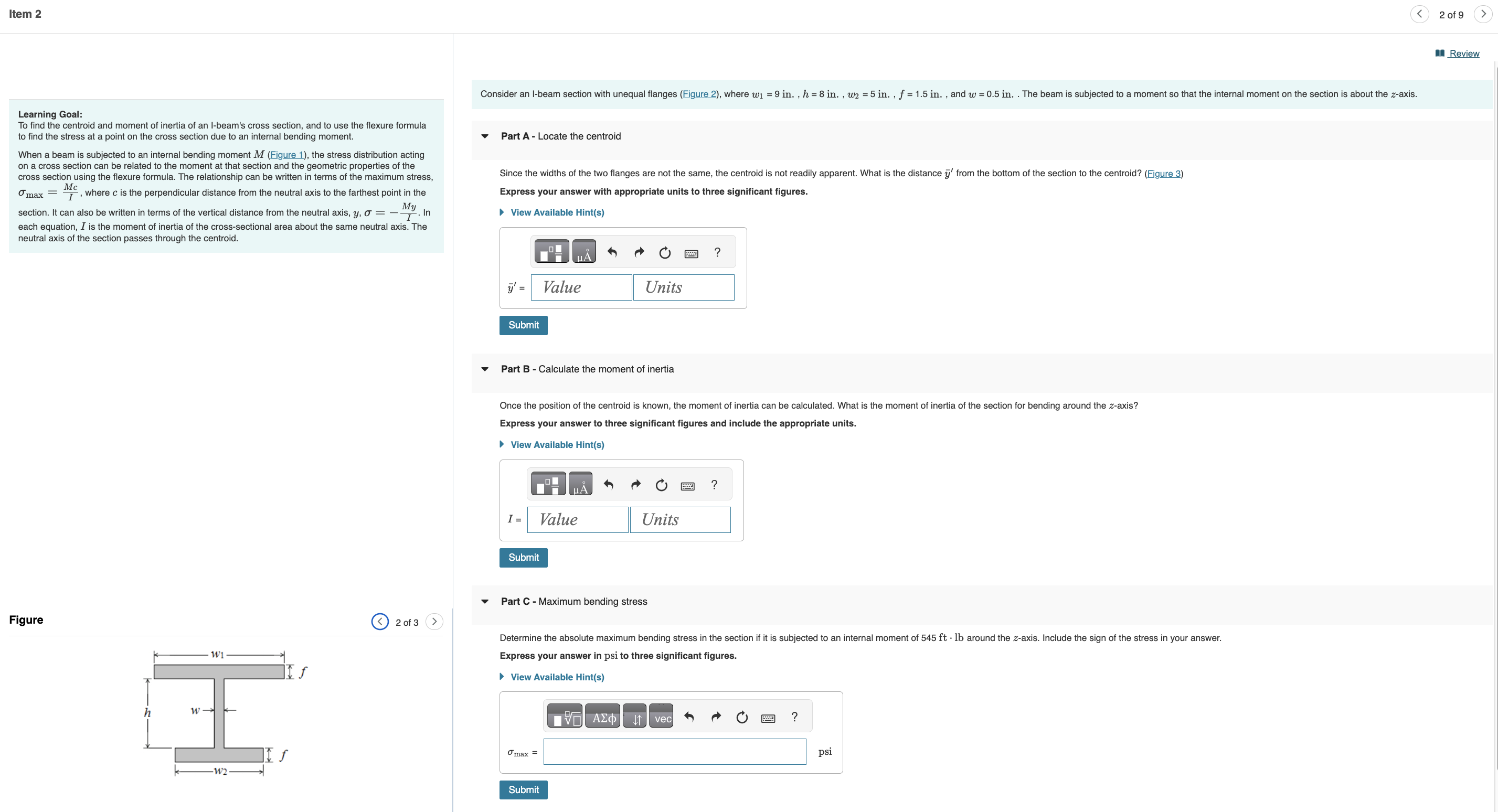
Consider an I$-$beam section with unequal flanges $($Figure $2),$ where $\backslash ($ w$\_\{1\}=9\backslash$mathrm$\{$in$\}\backslash ),\backslash ($ h$=8\backslash$mathrm$\{$in$\}\backslash ).,\backslash ($ w$\_\{2\}=5\backslash$mathrm$\{$in$\}.,$ f$=1\mathrm{.}5\backslash$mathrm$\{$in$\}\backslash ),$ and $\backslash ($ w$=0\mathrm{.}5\backslash$mathrm$\{$in$\}\backslash )..$ The beam is subjected to a moment so that the internal moment on the section is about the $\backslash ($ z $\backslash )-$axis.

Learning Goal:

To find the centroid and moment of inertia of an I$-$beam's cross section, and to use the flexure formula to find the stress at a point on the cross section due to an internal bending moment.

When a beam is subjected to an internal bending moment $\backslash ($ M $\backslash )($Figure $1),$ the stress distribution acting on a cross section can be related to the moment at that section and the geometric properties of the on a cross section can be related to the moment at that section and the geometric properties of the cross section using the flexure formula. The relationship can be written in terms of the maximum stress,

$\backslash (\backslash$sigma$\_\{\backslash$max $\}=\backslash$frac$\{$M c$\}\{$I$\}\backslash ),$ where $\backslash ($ c $\backslash )$ is the perpendicular distance from the neutral axis to the farthest point in the section. It can also be written in terms of the vertical distance from the neutral axis, $\backslash ($ y$,\backslash$sigma$=-\backslash$frac$\{$M y$\}\{$I$\}\backslash ).$ In each equation, $\backslash ($ I $\backslash )$ is the moment of inertia of the cross$-$sectional area about the same neutral axis. The neutral axis of the section passes through the centroid.

Figure $2$ of $3$