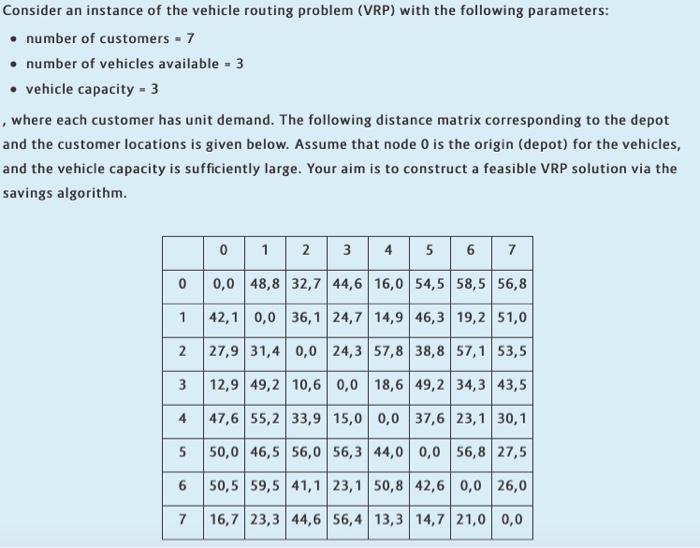
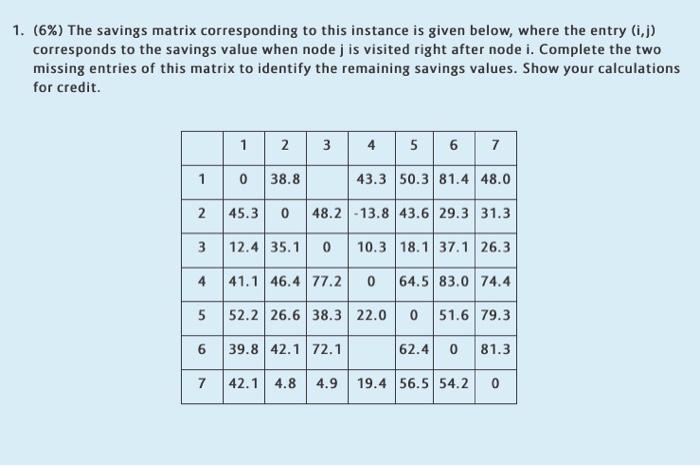
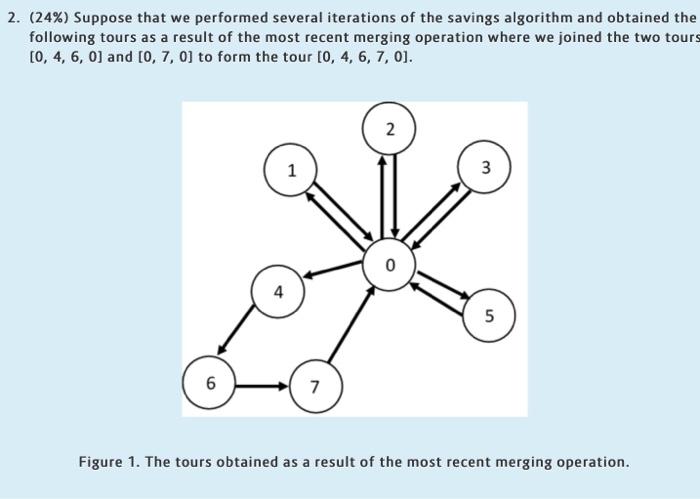
Consider an instance of the vehicle routing problem (VRP) with the following parameters: number of customers - 7 number of vehicles available - 3 vehicle capacity = 3 , where each customer has unit demand. The following distance matrix corresponding to the depot and the customer locations is given below. Assume that node 0 is the origin (depot) for the vehicles, and the vehicle capacity is sufficiently large. Your aim is to construct a feasible VRP solution via the savings algorithm 0 1 2 3 4 5 6 7 o 0,0 48,8 32,744,6 16,0 54,5 58,5 56,8 1 42,1 0,0 36,124,7 14,9 46,3 19,2 51,0 2. 27,9 31,4 0,0 24,3 57,8 38,8 57,1 53,5 3 12,9 49,2 10,6 0,0 18,6 49,234,3 43,5 4 47,6 55,2 33,9 15,0 0,0 37,6 23,130,1 5 50,0 46,556,0 56,3 44,0 0,0 56,8 27,5 6 LO 50,5 59,5 41,123,1 50,8 42,6 0,0 26,0 7 16,723,3 44,656,4 13,3 14,7 21,0 0,0 1. (6%) The savings matrix corresponding to this instance is given below, where the entry (ij) corresponds to the savings value when nodej is visited right after node i. Complete the two missing entries of this matrix to identify the remaining savings values. Show your calculations for credit. 1 2 3 4 5 6 7 0 38.8 43.3 50.3 81.4 48.0 45.3 0 48.2-13.8 43.6 29.3 31.3 1 2 3 4 3 12.4 35.1 0 10.3 18.137.1 26.3 41.1 46.477.2 0 64.583.0 74.4 5 52.226.6 38.3 22.0 0 51.6 79.3 6 39.8 42.172.1 62.4 0 81.3 7 7 42.1 4.8 4.9 19.4 56.5 54.2 0 2. (24%) Suppose that we performed several iterations of the savings algorithm and obtained the following tours as a result of the most recent merging operation where we joined the two tours [0, 4, 6, 0] and [0, 7, 0] to form the tour (0, 4, 6, 7, 0). 2 1 1 3 4 5 6 7 Figure 1. The tours obtained as a result of the most recent merging operation. Starting with the tours given in Figure 1, continue to apply the savings algorithm until a feasible VRP solution is found. (Hint: You need to iterate until the number of tours is equal to the number of vehicles, which is three in this example. When checking whether you can merge two tours, be careful about the total number of customers in those two tours; if the total number exceeds the vehicle capacity, merging is not possible.). Show each of your iterations and progress of the algorithm in detail. Present your final result clearly. Consider an instance of the vehicle routing problem (VRP) with the following parameters: number of customers - 7 number of vehicles available - 3 vehicle capacity = 3 , where each customer has unit demand. The following distance matrix corresponding to the depot and the customer locations is given below. Assume that node 0 is the origin (depot) for the vehicles, and the vehicle capacity is sufficiently large. Your aim is to construct a feasible VRP solution via the savings algorithm 0 1 2 3 4 5 6 7 o 0,0 48,8 32,744,6 16,0 54,5 58,5 56,8 1 42,1 0,0 36,124,7 14,9 46,3 19,2 51,0 2. 27,9 31,4 0,0 24,3 57,8 38,8 57,1 53,5 3 12,9 49,2 10,6 0,0 18,6 49,234,3 43,5 4 47,6 55,2 33,9 15,0 0,0 37,6 23,130,1 5 50,0 46,556,0 56,3 44,0 0,0 56,8 27,5 6 LO 50,5 59,5 41,123,1 50,8 42,6 0,0 26,0 7 16,723,3 44,656,4 13,3 14,7 21,0 0,0 1. (6%) The savings matrix corresponding to this instance is given below, where the entry (ij) corresponds to the savings value when nodej is visited right after node i. Complete the two missing entries of this matrix to identify the remaining savings values. Show your calculations for credit. 1 2 3 4 5 6 7 0 38.8 43.3 50.3 81.4 48.0 45.3 0 48.2-13.8 43.6 29.3 31.3 1 2 3 4 3 12.4 35.1 0 10.3 18.137.1 26.3 41.1 46.477.2 0 64.583.0 74.4 5 52.226.6 38.3 22.0 0 51.6 79.3 6 39.8 42.172.1 62.4 0 81.3 7 7 42.1 4.8 4.9 19.4 56.5 54.2 0 2. (24%) Suppose that we performed several iterations of the savings algorithm and obtained the following tours as a result of the most recent merging operation where we joined the two tours [0, 4, 6, 0] and [0, 7, 0] to form the tour (0, 4, 6, 7, 0). 2 1 1 3 4 5 6 7 Figure 1. The tours obtained as a result of the most recent merging operation. Starting with the tours given in Figure 1, continue to apply the savings algorithm until a feasible VRP solution is found. (Hint: You need to iterate until the number of tours is equal to the number of vehicles, which is three in this example. When checking whether you can merge two tours, be careful about the total number of customers in those two tours; if the total number exceeds the vehicle capacity, merging is not possible.). Show each of your iterations and progress of the algorithm in detail. Present your final result clearly