Consider the 2-floor, hexagonally shaped building depicted below. Assume that the blue edges represent the only possible ways to navigate from one corner of the building to another, including via an adjacent corner on the same floor, or by going up/down one of the elevators on the west or east side of the building. (Ex: from the corner denoted by "a", it is possible to walk to the corners denoted by "b", "f", or "t.")

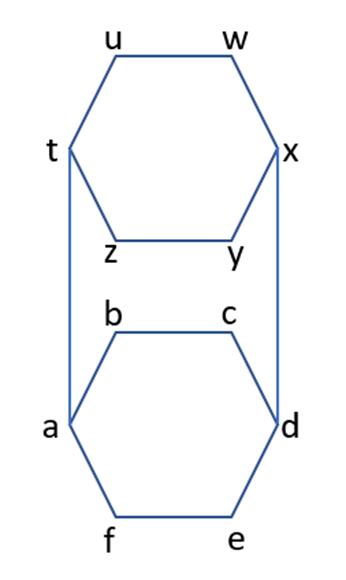
(a) Let G be a graph representing the building’s structure. Write out set V(G) representing the twelve corners of the building as vertices, and set E(G) representing all valid edges that walk from one corner to another.
(b) Is it possible to start at the corner denoted as “b” in the building, traverse every available edge in E(G) once and only once, and arrive back at “b”? Explain your answer.
(c) Repeat (b) but this time you don’t have to return to the corner you started at after traversing all edges.
(d) Is it possible to traverse the building while visiting every corner once and only once and return to the same corner that you started at? Explain your answer.
 

t a u 'N b f W C e X d