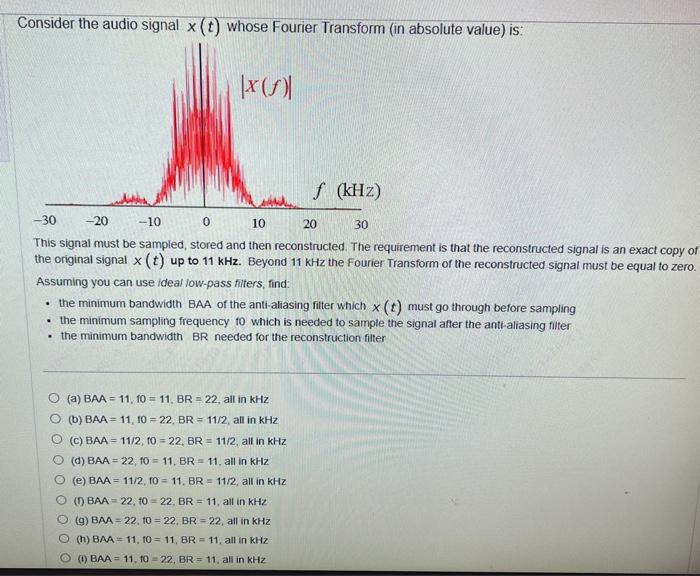
Consider the audio signal X(t) whose Fourier Transform (in absolute value) is: |x (6) 0 f (kHz) -30 -20 -10 10 20 30 This signal must be sampled, stored and then reconstructed. The requirement is that the reconstructed signal is an exact copy of the original signal X(t) up to 11 kHz. Beyond 11 kHz the Fourier Transform of the reconstructed signal must be equal to zero. Assuming you can use ideal low-pass filters, find: the minimum bandwidth BAA of the anti-aliasing filter which (t) must go through before sampling the minimum sampling frequency to which is needed to sample the signal after the anti-aliasing filter the minimum bandwidth BR needed for the reconstruction filter (a) BAA = 11.10 = 11. BR = 22. all in kHz (b) BAA= 11. 10 = 22. BR = 11/2, all in KHz O (C) BAA = 11/2, 10 = 22. BR = 11/2, all in KHz (d) BAA = 22, 10 = 11. BR = 11. all in kHz (e) BAA = 11/2, 10 = 11. BR = 11/2. all in KHz OO) BAA = 22, 1022, BR = 11, all in KHz (9) BAA=22, 10 = 22, BR = 22, all in KHz 0 (h) BMA 11.10 = 11, BR = 11. all in KHz OO) BAA = 11.10 = 22, BR = 11. all in KHz