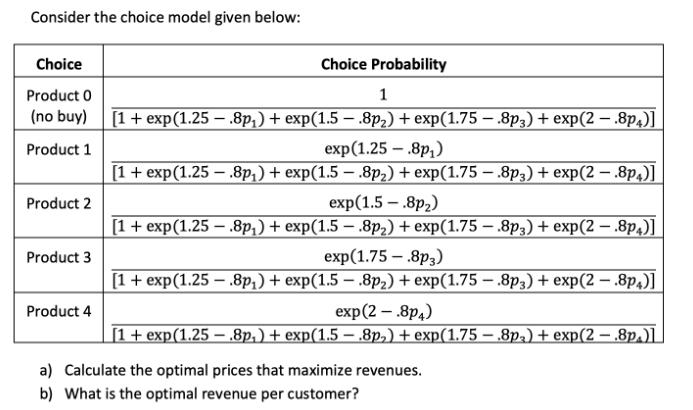
Consider the choice model given below: Choice Choice Probability Product 0 1 (no buy) [1+ exp(1.25 .8p) + exp(1.5 .8p) + exp(1.75 .8p3) + exp(2 .8p)] Product 1 Product 2 Product 3 Product 4 exp(1.25 - .8p) [1 + exp(1.25-8p) + exp(1.5 - 8p) + exp(1.75- 8p3) + exp(2.8p4)] exp(1.5 - 8p) [1 + exp(1.25.8p) + exp(1.5 - 8p) + exp(1.75 - 8p3) + exp(2 .8p4)] exp(1.75- 8p3) [1 + exp(1.25.8p) + exp(1.5 - 8p) + exp(1.75 - 8p3) + exp(2.8p4)] exp(2 - .8p4) [1 + exp(1.25.8p) + exp(1.5 .8p) + exp(1.75 8p) + exp(2 .8p.)] a) Calculate the optimal prices that maximize revenues. b) What is the optimal revenue per customer?