Consider the continuously compounded yield curve y(t,T)=0.045-0.04e^(-0.5)(T-t)

(a) Determine the purchase price of a zero coupon bond that matures after 4 years if its face value is $100.

(b) Consider the cash flows (payments) [ C1, C2, C3] = [ $350, $450, $400] at times [ T1, T2, T3] = [ 1.75, 2.25, 3.75] (in years).

(i) Determine the present value of the cash flow stream.

(ii) Determine the duration of the cash flow stream to 3 decimals

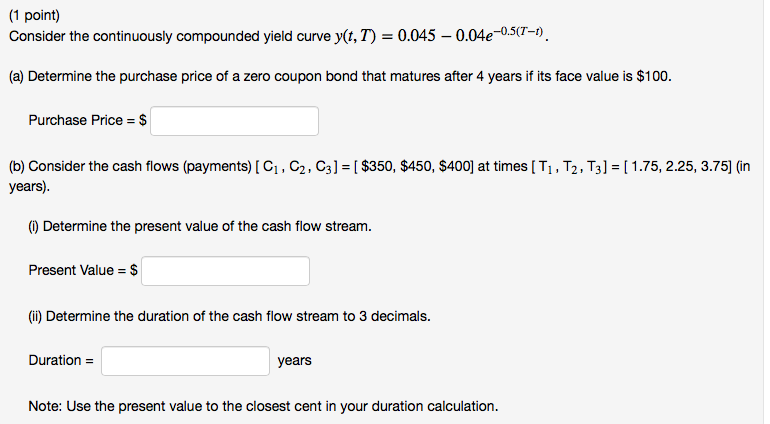
(1 point) Consider the continuously compounded yield curve y(t, 7) = 0.045 - 0.04e-0.5(7-1). (a) Determine the purchase price of a zero coupon bond that matures after 4 years if its face value is $100. Purchase Price = $ (b) Consider the cash flows (payments) [ C1 , C2, C3] = [ $350, $450, $400] at times [ T1 , T2, T3] = [ 1.75, 2.25, 3.75] (in years). (i) Determine the present value of the cash flow stream. Present Value = $ (ii) Determine the duration of the cash flow stream to 3 decimals. Duration = years Note: Use the present value to the closest cent in your duration calculation