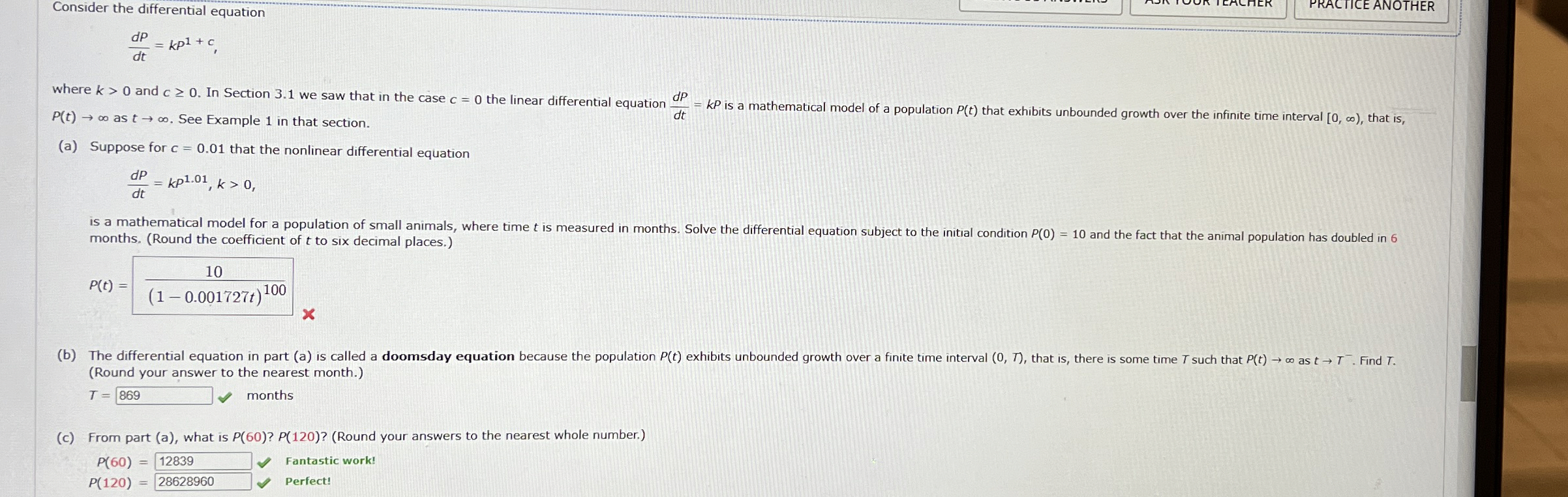
Consider the differential equation

$\frac{dP}{dt}=k{P}^{1+c}P(t)$ as $t.$ See Example $1$ in that section.

$($a$)$ Suppose for $c=0\mathrm{.}01$ that the nonlinear differential equation

$\frac{dP}{dt}=k{P}^{1\mathrm{.}01},k>0$ months. $($Round the coefficient of $t$ to six decimal places.$)$

$P(t)=\frac{10}{(1-0\mathrm{.}001727t{)}^{100}}($Round your answer to the nearest month.$)$

$T=|$ months

$($c$)$ From part $($a$),$ what is $P(60)?P(120)?($Round your answers to the nearest whole number.$)$

$P(60)=$

$P(120)=28628960$ Fantastic