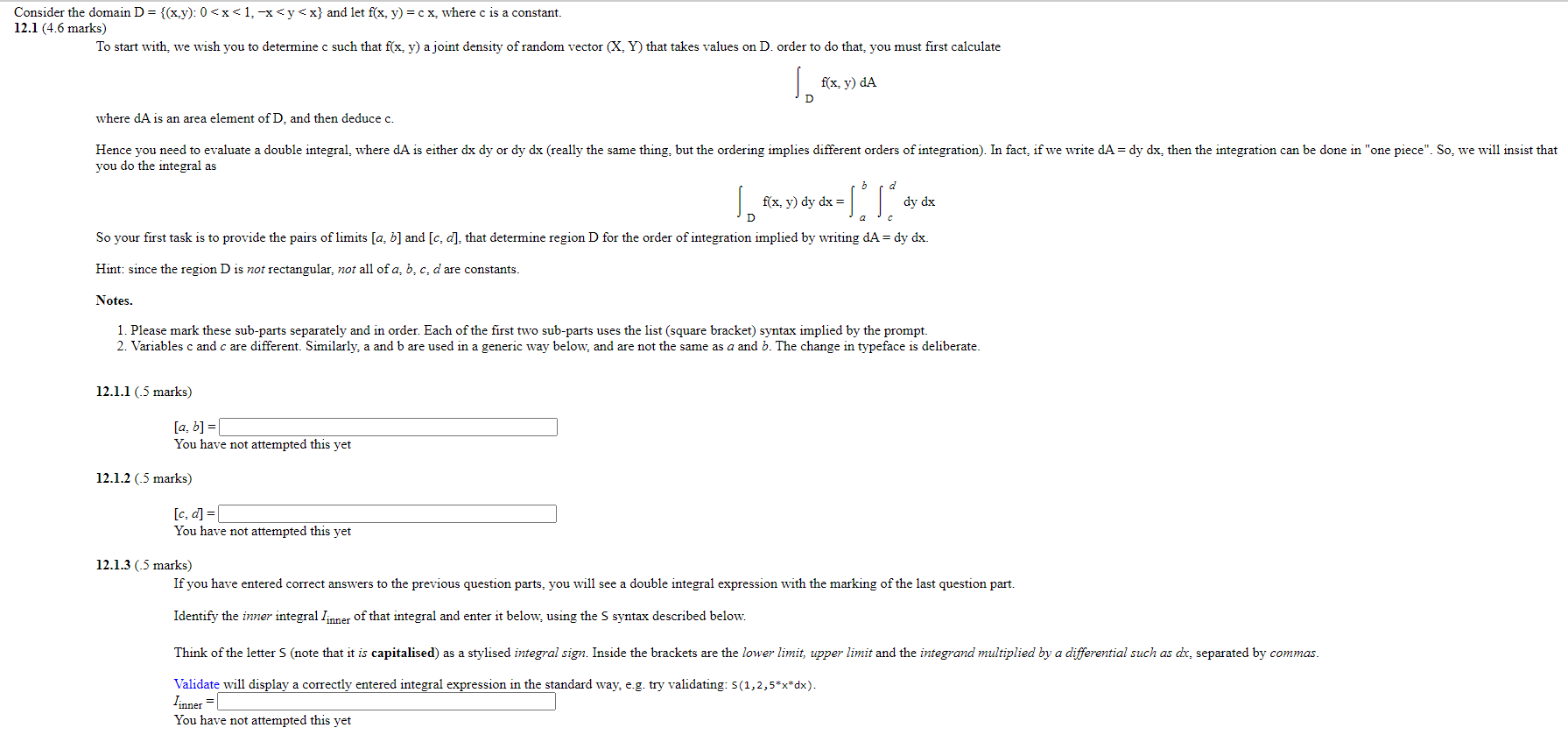
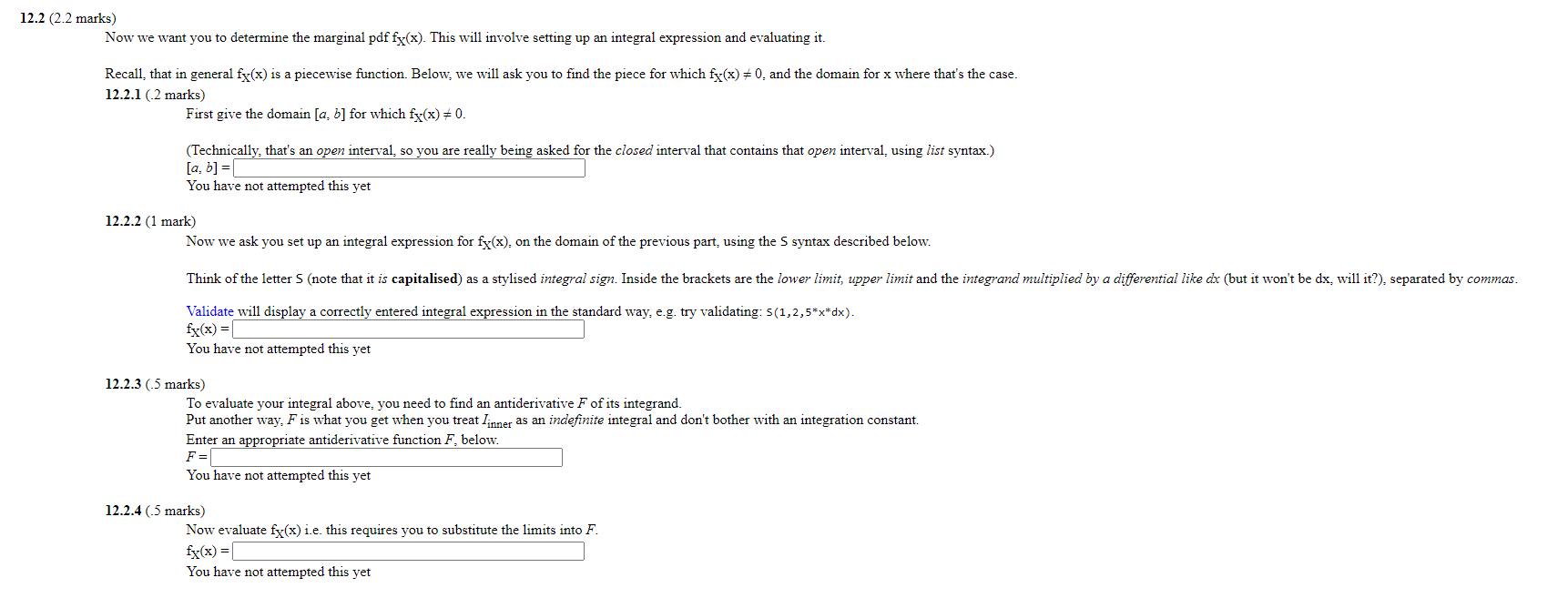
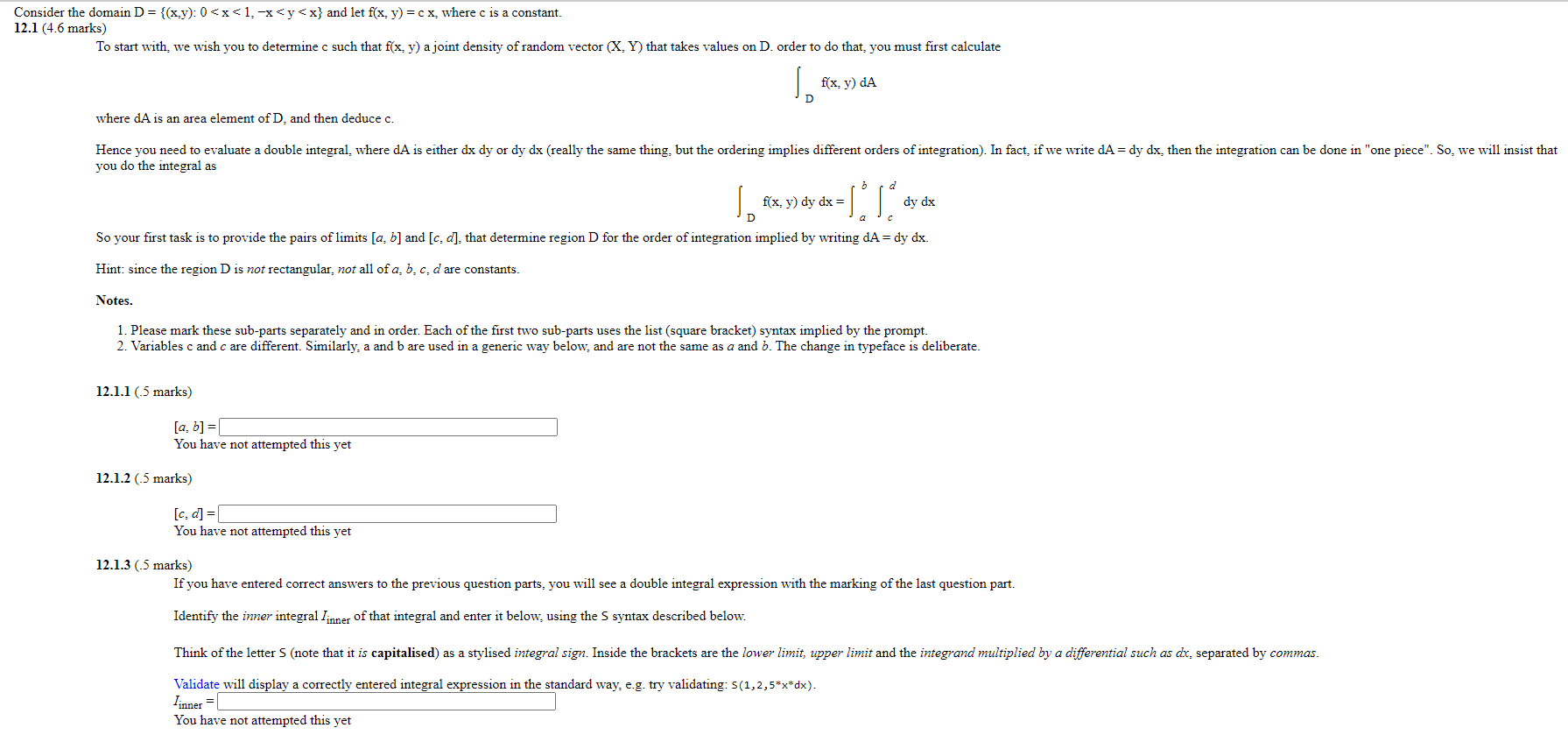
Question: Consider the domain D = {(x.y): 0 0.7) = You have not attempted this yet Consider the domain D = {(x:y): O < x <


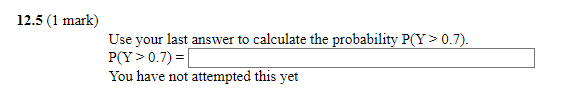

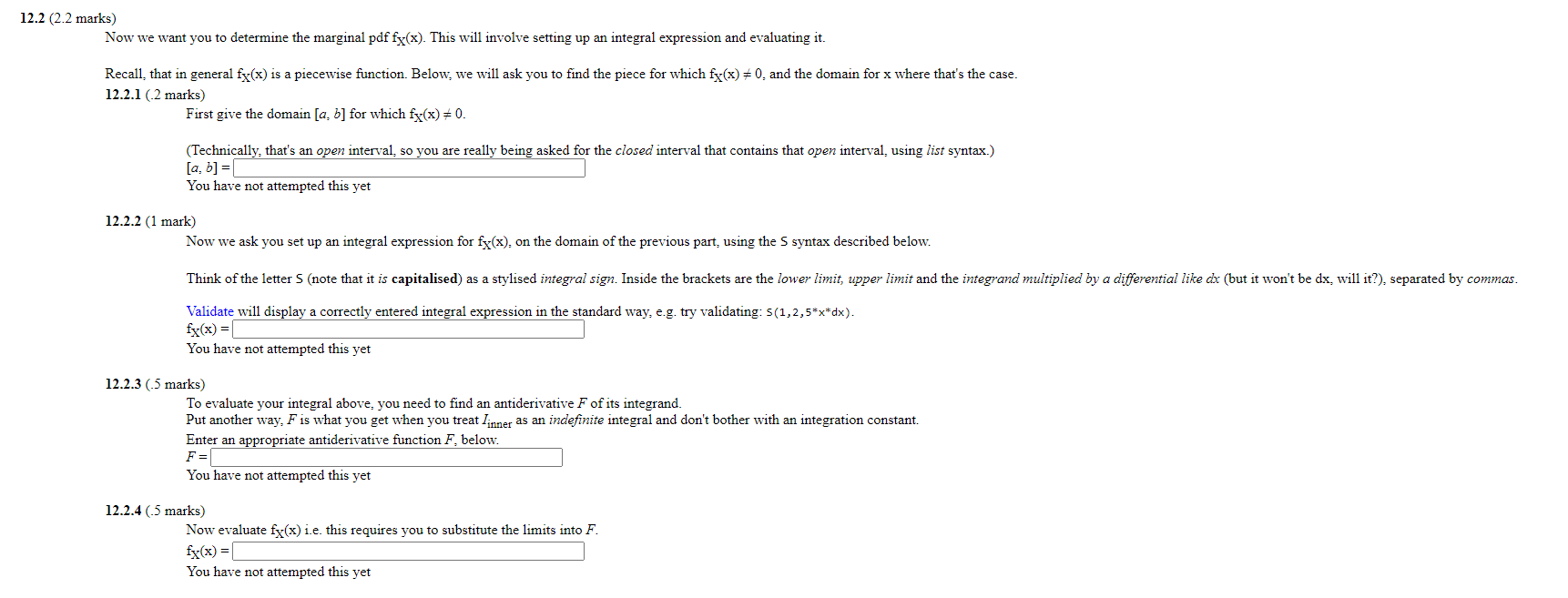

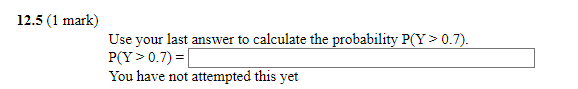
Consider the domain D = {(x.y): 0 0.7) = You have not attempted this yet
Consider the domain D = {(x:y): O < x < 1 : x < y < x} and let f(x: y) = c x: where c is a constant. 12.1 (4.6 marks) To start we wish you to determine c such that f(x: y) ajoint density of random vector (X: Y) that takes values on D order to do that: you must first calculate fix: y) dA where dA is an area element of D: and then deduce c. Hence you need to evaluate a double integral: where dA is either dx dy or dy dx (really the same thing: but the ordering implies different orders of integration). In fact: if we write dA you do the integral as f(x: y) dy dx dy dx So your first task is to provide the pairs of limits [a: b] and [c: that determine region D for the order of integration implied by uriting dA dy dx_ Hint: since the region D is not rectangular: not all of a: b: c: d are constants. Notes. 1. Please mark these sub-parts separately and in order Each of the first two sub-parts uses the list (square bracket) syntax implied by the prompt. 2. Variables c and c are different. Similarly: a and b are used in a generic way below: and are not the same as a and b _ The change in typeface is deliberate. 12.1.1 (5 marks) You have not attempted this yet 12.1.2 (5 marks) You have not attempted this yet 12.1.3 (5 marks) If you have entered correct answers to the previous question parts: you will see a double integral expression with the marking of the last question part. Identify the inner integral 1- of that integral and enter it below: using the S syntax described below. dy clx: then the integration can be done in "one piece' _ So: we will insist that Think of the letter S (note that it is capitalised) as a stylised integral sign. Inside the brackets are the lower limit, upper limit and the integrand multiplied by a differential such as ax, separated by commas. Validate will display a correctly entered Integral expression in the standard way: e.g. try validating: s (1, 2 , You have not attempted this yet
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


